Now, let us suppose a famous sequence called as bitonic sequence and sort out the elements using a combinational circuit consisting of a set of comparators. The property of bitonic sequence is as follows:

Consider a series X= x0, x1, x2, x3, x4 ................... xn-1 such that condition 1:either x0, x1, x2, x3, x4 ................... xi is a monotonically increasing sequence and xi+1, xi+2,  ................... xn-1  is a monotonically decreasing sequence or condition 2: there exists a cyclic shift of the series  x0, x1, x2, x3, x4 ................... xn-1 such that the resulting series satisfies the condition 1.

Let us take a few examples of bitonic series: B1= 4,7,8,9,11,6,3,2,1 is bitonic series

B2= 12,15,17,18,19,11,8,7,6,4,5 is bitonic series

In order to give a solution to such a bitonic sequence, various phases of comparators are needed. The basic approach followed for solving such a difficulty is as given:

 Let us say we have a bitonic series X= x0, x1, x2, x3, x4 ................... xn-1 with the property that first n/2 elements are monotonically increasing elements are monotonically increasing like x0< x1< x2< x3< x4 ... xn/2+1> ...>xn-1.  After that, these patterns are compared with the help of a comparator as follows:

Y= min(x0, xn/2), min(x1, xn/2+1), min(x2, xn/2+2), ............. Min (xn/2-1, xn-1)

Z= max(x0, xn/2), max (x1, xn/2+1), max (x2, xn/2+2), ............. max (xn/2-1, xn-1)

After the above discussed iteration, the two new bitonic series are produced and the method is called as bitonic split. After that, a recursive operation on these two bitonic sequences is processed until we are able to achieve the sorted list of elements. The exact algorithm for sorting the bitonic series is as follows:

Sort_Bitonic (X)

// Input: N Numbers following the bitonic property

// Output: Sorted List of numbers

1) The Sequence, i.e. X is transmitted on the input lines of the combinational circuit which consists of a variety of set of comparators.

2) The sequence X is divided into two sub-bitonic series say, Y and Z, with the help of a method known as bitonic split.

3) Recursively implements the bitonic split on the sub series, i.e. Y and Z, until the size

Of subsequence reaches to a level of 1.

1) The sorted series is achieved after this level on the output lines.

With the help of a diagram to demonstrate the concept of sorting using the comparators.

Example 1: Consider a unsorted list having the element values as

{3,5,8,9,10,12,14,20,95,90,60,40,35,23,18,0}

List is to be sorted in ascending order. To sort this list, in the first stage comparators of order 2 (i.e. having 2 input and 2 output) will be used. Similarly, 2nd stage will consist of 4, input comparators, 3rd stage 8 input comparator and 4th stage a 16 input comparator.

Let us consider an example with the help of a diagram to illustrate the concept of sorting using the comparators.

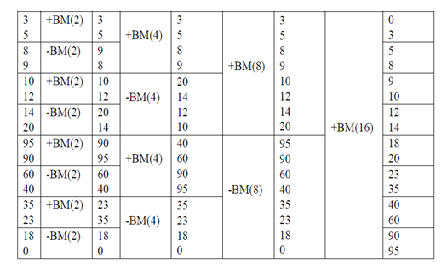
                                                          Sorting using Combinational Circuit