Solve out the following system of equations by using augmented matrices.

3x - 3 y - 6 z = -3

2x - 2 y - 4 z = -2

-2x + 3 y + z = 7

Solution

Notice that this system is approximately identical to the system in earlier example. The only difference is the number to the right of the equal sign in the second equation.  In this system it is two and in the previous example it was ten.  Altering that one number totally changes the type of solution that we're going to get.  Frequently this kind of simple change won't influence the type of solution that we get, however in some rare cases it can.

Since the first two steps of the procedure are identical to the previous part we won't discuss them. Here they are.

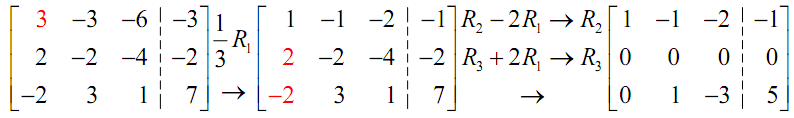
We've got a row of all zeroes thus we instantly know that we've got infinitely several solutions. Unlike the two equation case we aren't going to stop however.  This looks like with a couple of row operations we can make the second column look as it is assumed to in the final form so let's do that.

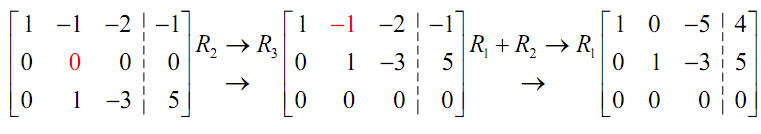
In this case we were capable to make the second column look as it's assumed to and the third column will never look accurate.  Though, this is possible that the condition could be reversed and it would be the third column which we can make look correct and the second wouldn't look right. Every system is different.

Once we reach this point we go back to equations.

             x - 5z = 4

             y - 3z = 5

Now, both of these equations have a z and thus we'll move that to the other side in each equation.

                           x + 5z = 4

                           y + 3z = 5

It means that we get to pick the value of z for free & we'll write the solution as,

x = 5t + 4

y =3t + 5        

z = t

 where t refer to any real number

As there are an infinite number of ways to select t there are an infinite number of solutions to this system.