A producer of furniture manufactures two products - tables and chairs. Processing of these products is done on two machines A and B. A chair needs 2 hours on machine A and 6 hours on machine B. A table needs 5 hours on machine A and no time on machine B. There are 16 hours of time per day accessible on machine A and 30 hours on machine B. Profit earned by the manufacturer from a chair and a table is Rs 2 and Rs 10 correspondingly. What must be the everyday production of each of two products?
Answer
Assume x1 indicates the number of chairs
Assume x2 indicates the number of tables
|
|
Chairs
|
Tables
|
Availability
|
|
Machine A
Machine B
|
2
6
|
5
0
|
16
30
|
|
Profit
|
Rs 2
|
Rs 10
|
|
LPP
Max Z = 2x1 + 10x2
Subject to
2x1+ 5x2 ≤ 16
6x1 + 0x2 ≤ 30
x1 ≥ 0 , x2 ≥ 0
Solve graphically
The first constraint 2x1+ 5x2 ≤ 16, can be written in the form of equation
2x1+ 5x2 = 16
Place x1 = 0, then x2 = 16/5 = 3.2
Place x2 = 0, then x1 = 8
The coordinates are (0, 3.2) and (8, 0)
The second constraint 6x1 + 0x2 ≤ 30, can be written in the form of equation
6x1 = 30 → x1 =5
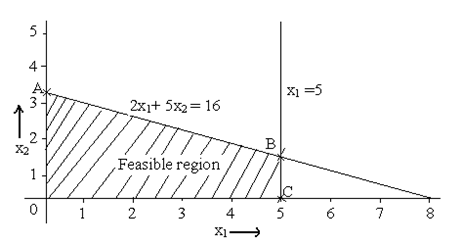
The corner positions of feasible region are A, B and C. So the coordinates for the corner positions are
A (0, 3.2)
B (5, 1.2) (Solve the two equations 2x1+ 5x2 = 16 and x1 =5 to obtain the coordinates)
C (5, 0)
We are given that Max Z = 2x1 + 10x2
At A (0, 3.2)
Z = 2(0) + 10(3.2) = 32
At B (5, 1.2)
Z = 2(5) + 10(1.2) = 22
At C (5, 0)
Z = 2(5) + 10(0) = 10
Max Z = 32 and x1 = 0, x2 = 3.2
The manufacturer must manufacture about 3 tables and no chairs to obtain the max profit.