This chapter introduces mixed strategies and the methods used to solve for mixed strategy equilibria. Students are likely to accept the idea of randomization more readily if they think of it themselves. Here is one way to lead them to the idea: Draw or project the game table for the tennis game in Chap- ter 5 (Figure 5.1 or Figure 4.14), and ask one student to put herself in the shoes of Seles and think whether she would choose cross-court or down the line. Usually the answer will be one or the other, with some technical justification. Then ask another student how she would react if she were Hingis. Proceeding this way, get them to realize the importance of keeping the other guessing. Build this into the formal idea that randomization improves your maximin or minimax pay- off. Similarly, to get across the idea of an equilibrium in mixed strategies, a good way to start is by getting students to trace out the succession of best responses that goes full circle in the tennis table or equivalent.

Once you have provided some intuition or motivation for the use (and usefulness) of mixed strategies, you can approach the problem of solving for the equilibrium mixtures. Stu- dents will quickly grasp the ideas that mixed strategies are a special  case  of  continuous  strategies  in  which  players choose a value for p-the probability of using one of the two possible actions-from the interval [0, 1] and that the value of p at 0 or 1 coincide with the use of a pure strategy. Given this, we have been most successful starting with zero- sum games and the minimax analogy-arguing that the row for the p-mix and the column for the q-mix contain payoffs for all possible values of p against the rival's pure strategies. These payoffs are represented as functions of p or q and, as such, can be graphed. Then the maximin/minimax process implies that the row player's maximin occurs at that value of p which maximizes the entire set of minimum payoffs; graphically, this is the p value at the tip of the inverted V of minimum payoffs. Similarly for the column players. Stu- dents who have already learned the minimax method accept the logic of this process readily.

This method, which we call the prevent-exploitation method, works only for games in which a rival's best choice for herself is the worst choice for you, so it works only in zero-sum games. However, once you have derived the equi- librium mixtures, you can show that these have an additional feature; they serve to keep the opponent indifferent between her two pure strategies. This is the logic that we employ when searching for mixed-strategy equilibria in non-zero-sum games, in our keep-the-opponent-indifferent method; you can show the result arises in the zero-sum case and argue that equilibrium mixes must, in general, achieve this indifference property. Then it is much easier to show how the non-zero-sum analysis proceeds.

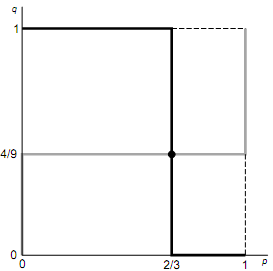
For games with multiple equilibria in pure strategies, as well as a mixed-strategy equilibrium, it is useful to show the best-response curve diagram for p and q. This diagram allows students to see all of the Nash equilibria of such games in one place; pure-strategy equilibria occur when the best-response curves meet at one or more of the corners, and mixed-strategy equilibria occur when the curves intersect at values of p and q in between 0 and 1. In games in which players' interests are opposed, like chicken, the pure-strategy equilibria occur at the top left, (0, 1), and bottom right, (1, 0), of the diagram, while in games in which the players' interests are aligned, like assurance games, the pure-strategy equilibria occur at the origin, (0, 0), and at the upper right corner, (1, 1).

One example that we have used successfully in class when covering basic 2-by-2 mixing is based on the Sherlock Holmes-Moriarty story that is told in John von Neumann and Oskar Morganstern's, Theory of Games and Economic Behavior. The gist of the story is that Holmes is trying to get from London via Canterbury to Dover by train (and hence to the Continent) in order to escape from Moriarty. Moriarty has seen Holmes enter the train and can presum- ably get another himself. Each must then decide whether to go all the way to Dover or to get out at the single intermedi- ate station at Canterbury; Holmes would prefer to make the opposite decision from Moriarty while Moriarty would prefer to make the same decision as Holmes.

Many students will not have read the story. For that matter, many may not be entirely familiar with the geography of England and France. [One of us (Dixit) has used a schematic drawing of the southeast corner of England showing the cities in question, the Channel, and the northern coast of France to make a joke about the modern student's ignorance of geog- raphy.] It may be worthwhile to add a bit of background related to Conan Doyle and the Holmes stories as well as Moriarty, who was not only the "godfather" of crime in London but a professor of mathematics as well.

The payoff table we have used for this game is:

Min =   -0

Max = 75             Max = 100

The payoffs (which differ slightly from those found in von Neumann and Morganstern) are to Moriarty, who is most truly defeated if he exits at Canterbury to find that Holmes has continued safely on to Dover. The maximin of 0 does not equal the minimax of 75 here; the game has no equilibrium in pure strategies.

Moving on to consider mixed strategies, you can add a row for Moriarty's p-mix (see new payoff table below) and show how this new strategy allows Moriarty a way of improving his maximin payoff.

Min =      0

Min = - 50

Graphing Moriarty's payoffs against Holmes playing either Dover (-50 payoff at p = 0 and 75 payoff at p = 1) or Canterbury (100 payoff at p = 0 and 0 payoff at p = 1) allows you to show Moriarty's minimum payoff in the p-mix row as an inverted V on the graph. The maximin occurs at the inter- section of the two lines on the graph or at the value of p that solves 75p - 50(1 - p) = 100(1 - p); this value of p is 2/3. Moriarty's maximin payoff is 100(1 - p) (or -50(1 - p) + 75p) for p = 2/3 or 100/3, or 33 1.

Similar calculations can be done for Holmes in determin- ing his q-mix. You can show his mixture as a third column in the payoff table:

Max = 75

Max = 100

Max = ?

Graphing payoffs for Holmes against Moriarty playing his pure strategies as in Figure 5.5-using Moriarty's payoffs on the vertical axis (since Holmes gets the opposite) and q on the horizontal axis-allows you to show Holmes's maximum pay- offs as a V-shaped curve on the graph. The minimax value of q occurs at the intersection of the line representing Moriarty's choice of Dover (intercept 0 at q = 0 and 75 at q = 1) and the line representing Moriarty's choice of Canterbury (intercept 100 at q = 0 and -50 at q = 1); this value of q solves 75q = -50q + 100(1 - q). The minimax q in this case is 4/9; Holmes's minimax payoff, given this q, is 100/3, or 3313 .

In this example we see that the maximin payoff for Moriarty is equal to the minimax payoff for Holmes so that the mix- ture values we calculated above-p = 2/3 and q = 4/9- constitute a mixed-strategy equilibrium of the game. The best-response curves for the two players in this game are illustrated below; as shown, there is only one equilibrium of the game and that is the equilibrium in mixed strategies for p = 2/3 and q = 4/9.

You can extend this example to one in which Holmes has three pure strategies (although this goes beyond the scope of the analysis in von Neumann and Morganstern). Here Holmes has a third strategy, Emergency, which is to pull the train's emergency stop cord somewhere between Canterbury and Dover and to exit the train in this way. This strategy also forces Moriarty's trailing train to stop when it discovers the track ahead blocked. What are the payoffs from this new strategy? If Moriarty has gotten off at Canterbury, then for Holmes

Emergency is obviously better than Canterbury but worse than Dover because it still leaves him in the interior and not imme- diately on the boat to France; hence Emergency gets Holmes 0 if Moriarty gets off at Canterbury. But if Moriarty goes on to Dover, then his train will be held up due to the train emer- gency, and Holmes will find Emergency better than Dover but worse than Canterbury; we give Holmes a -20 (and Moriarty a 20) for this combination. Then we get the following payoff matrix, with a row added for Moriarty's p-mix:

Moriarty's minimum payoffs here no longer created an inverted-V shape as p varies from 0 to 1 because Holmes has three strategies. Rather we see Moriarty's set of minimum payoffs as the thick line in the diagram below:

Moriarty's payoff

The maximin value of p chosen by Moriarty is the one that yields the highest point on the thick line in the diagram, or the p at the intersection of Holmes's C(anterbury) and E(mergency) lines. That p solves 20p = 100(1 - p); p = 5/6 = 0.83. Moriarty's maximin payoff is 100/6 = 16.67.

Note that Moriarty's mix would be better against Holmes's use of the pure strategy Dover but Holmes does not use Dover in his mix. Holmes chooses C and E with probabilities z and (1 - z). The equilibrium value of z solves 0z + 20(1 - z) = 100z + 0(1 - z) which yields z = 20/120 = 1/6 = 0.17. Holmes's minimax payoff is 100/6 = 16.67, which is the same as Moriarty's maximin.