This is a project on music synthesis with sinusoids. The project requires programming effort in Matlab, a software package which is installed in the computer labs in the School of Engineering. You should start by familiarizing yourself with Matlab by using its Help resources and by reading the additional documents on Blackboard. The project should be documented with a complete report, edited and submitted electronically via Blackboard. A good report should include the following items: a cover sheet, commented Matlab code, explanations of your approach, conclusions and any additional tweaks that you implemented for the synthesis. Since the project must be evaluated by listening to the quality of the synthesized song, in addition to the report, the final program should also be submitted via Blackboard, along with the report.

Overview

We have spent some time learning about the properties of sinusoidal waveforms of the form

x(t)= A cos(w0t + ?)

In this project you will synthesize waveforms composed of sums of sinusoidal signals of this form, sample them, and then reconstruct them for listening. We will use combinations of the basic sinusoid (1) to synthesize the following signals:

1. Sine waves at a specific frequency played through a D/A converter.

2. Sinusoids that create a synthesized version of the piece Twinkle, Twinkle, Little Star.

The primary objective of the project is to establish the connection between musical notes, their frequencies and sinusoids. By taking this challenge you will hopefully be motivated to learn more about the spectral representation of signals-a topic that underlies this entire unit.

Warm-up: Music Synthesis

In this project, the sine waves and music signals will be created with the intention of playing them out through a speaker. Therefore, it is necessary to take into account the fact that a conversion is needed from the digital samples which are numbers stored in the computer memory to the actual voltage waveform that will be amplified for the speakers. The digital to- analog conversion process has a number of aspects, but in its simplest form the only thing you need to worry about at this point is that the time spacing (Ts) between the signal samples must correspond to the rate of the D-to-A hardware that is being used. From Matlab, the sound output is done by the sound(x,fs) function which does support variable sampling rate. A convenient choice for the D-to-A conversion rate is 8000 samples per second, so Ts =1/8000 seconds. In some cases, it will also be necessary to scale the vector x so that it lies between ±1. In Matlab, there is a function, soundsc(x,fs), which performs that scaling.

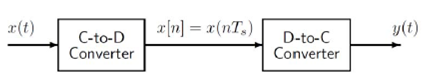
The idealized process of sampling a signal and the subsequent reconstruction of the signal from its samples is depicted in Fig. 1. This figure shows a continuous-time input signal x(t), which is sampled by the continuous-to-discrete (C-to-D) converter to produce a sequence of samples x[n]= x(nTs), where n is the integer sample index and Ts is the sampling period. The sampling rate is fs =1/Ts. The ideal discrete-to-continuous (D-to-C) converter takes the input samples and interpolates a smooth curve between them. The Sampling Theorem tells us that if the input is a sum of sine waves, then the output y(t) will be equal to the input x(t) if the sampling rate is more than twice the highest frequency fmax in the input, i.e., fs > 2fmax. Most computers have a built-in analog-to-digital (A-to-D) converter and a digital-to-analog (D-to-A) converter (usually on the sound card). These hardware systems are physical realizations of the idealized concepts of C-to-D and D-to-C converters, respectively, and for purposes of this lab we will assume that they are perfect realizations.

(a) The ideal C-to-D converter will be implemented in Matlab by taking the formula for the continuous-time signal and evaluating it at the sample times, nTs. To begin, compute a vector x1 of samples of a sinusoidal signal with A = 100, w0 = 2p(1100), and ? = 0. Use a sampling rate of 8000 samples/second, and compute a total number of samples equivalent to 2 seconds time duration. You may find it helpful to know that the Matlab statement tt=(0:0.01:3); would create a vector of numbers from 0 through 3 with increments of 0.01. Therefore, it is only necessary to determine the time increment needed to obtain 8000 samples in one second. Using sound() play the resulting vector through the D-to-A converter of your computer.

Listen to the output.

(b) Now compute a vector x2 of samples (again, 2 seconds time duration) of the sinusoidal signal for the case A = 100, w0 = 2p(1650), and ? = p/3. Listen to the signal reconstructed from these samples. Put both signals together in a new vector defined with the following Matlab statement (assuming that both x1 and x2 are row vectors): xx = [x1 zeros(1,2000) x2]; Listen to this signal.

(c) Now send the vector xx to the D-to-A converter again, but double the sampling rate in sound( ) to 16000 samples/second. Do not recompute the samples in xx, just tell the D-to-A converter that the sampling rate is 16000 samples/second. Observe how the duration and pitch of the signal changed.

The main section of this project will consist of synthesizing the notes of a well known piece of music. If you have little or no experience reading music, don't be intimidated. Only a little knowledge is needed to carry out this project. On the other hand, the experience of working in an application area where you must quickly acquire knowledge is a valuable one. Many real-world engineering problems have this flavour, especially in signal processing which has such a broad applicability in diverse areas such as geophysics, medicine, radar, speech, etc.

Since you will use sinusoidal tones to represent piano notes, a quick introduction to the frequency layout of the piano keyboard is needed. On a piano, the keyboard is divided into octaves-the notes in each octave being twice the frequency of the notes in the next lower octave. For example, the reference note is the A above middle-C which is usually called A- 440 (or A5) because its frequency is 440 Hz. Each octave contains 12 notes (5 black keys and 7 white) and the ratio between the frequencies of the notes is constant between successive notes. Thus this ratio must be 2^1/12. Since middle C is 9 keys below A-440, its frequency is approximately 261 Hz.

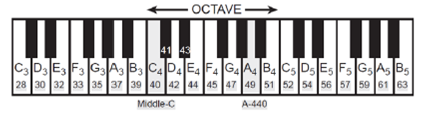
Musical notation shows which notes are to be played and their relative timing (half notes last twice as long as quarter notes, which, in turn, last twice as long as eighth notes). Figure 3 shows how the keys on the piano correspond to notes drawn in musical notation. Consult the additional document on Blackboard for more details.

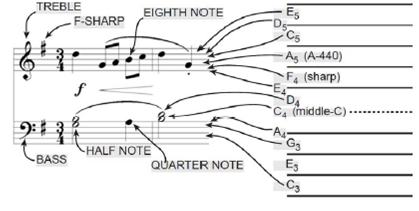
You can use the ratio 2^1/12 to calculate the frequency of notes anywhere on the piano keyboard. For example, the E-flat above middle-C (black key number 43) is 6 keys below A-440, so its frequency should be f = 440 × 2 -6/12 = 311 Hertz.

(a) Generate a sinusoid of 2 seconds' duration to represent the note E5 above A-440 (key number 56). Choose the appropriate values for Ts and fs. Remember that fs should be at least twice as high as the frequency of the sinusoid you are generating. Also, Ts and fs must "match" in order for the note played out of the D-to-A converter to sound correct.

(b) Now write an M-file to produce a desired note for a given duration. Your M-file should be in the form of a function called note.m. Your function should have the following form:

function tone = note(keynum,dur)

% NOTE Produce a sinusoidal waveform corresponding to a

% given piano key number

%

% usage: tone = note (keynum, dur)

%

% tone = the output sinusoidal waveform

% keynum = the piano keyboard number of the desired note

% dur = the duration (in seconds) of the output note

fs = 8000; % use 11025 Hz on PC/Mac, 8000 on UNIX

tt = 0:(1/fs):dur;

freq =

tone =

For the freq = line use the formulas based on 2^1/12 to determine the frequency for a sinusoid in terms of its key number. You should start from a reference note (middle-C or A-440 is recommended) and solve for the frequency based on this reference. For the tone = line, generate the actual sinusoid at the proper frequency and duration.

(c) The following is an incomplete M-file that will play scales:

For the tone = line, generate the actual sinusoid for keynum by making a call to the function note() written previously. Note that the code in play_scale.m allocates a vector of zeros large enough to hold the entire scale, then adds each note into its proper place in the vector xx.