RECENT DEVELOPMENT IN DEMAND ANALYSIS:

For many years economic theorists analysed the optimal behaviour of consumers while econometricians estimated consumer demand and expenditure relations, with little communication between the two. Theorists would provide examples that were of little aid for empirical work, and econometricians would estimates relations that had little connection with the theory of utility maximisation. Fortunately, as days passed on, the gap between theory and empirical evidence has lessened, and a number of theoretically strong examples that allow empirical estimation have been developed. In this section we present one of such examples.  

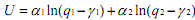
with the domain q₁>γ₁ and q₂>γ₂. The  γ's may be interpreted as minimum subsistence quantities and are positive. The α's are also positive. Applying the positive monotonic transformation U' = U/(α +α ) we get,  

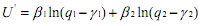
The coefficients β₁ and β₂ (β₁+ β₂ = 1) are called "share" parameters. The consumer's objective is to maximise her utility subject to budget constraint. So, she will try to solve the problem given below. 

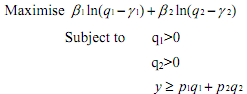
We set Lagrange function of the above maximisation exercise as  

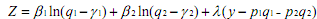
and set its first partial derivatives equal to zero (we assume interior solution of this maximisation problem):  

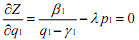
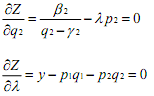
It can be easily verified that the second order condition for the maximisation is satisfied. By evaluating the above three equation one can also find out that the marginal utility of income is decreasing. 

Solving the above equations for optimal quantities gives the demand functions,  

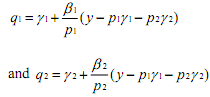
Multiplying the first equation of the above two demand functions by p₁ and the second by p₂ we get the expenditure functions  

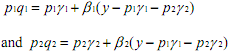
which are linear in income and prices, and thus suitable for linear regression analysis.