Now we have to look at rational expressions. A rational expression is a fraction wherein the numerator and/or the denominator are polynomials.  Here are some examples of rational expressions.

     6 /x -1          z ²  -1 /z ² + 5      m⁴ + 18m + 1/ m² - m - 6            4 x2 + 6 x -10/1

The last one might look a little strange as it is more commonly written 4 x² + 6 x -10 . But, it's significant to note that polynomials may be thought of as rational expressions if we have to, although they hardly ever are.

There is an unspoken rule while dealing along with rational expressions which now we need to address. While dealing with numbers we know that division with zero is not allowed. Well the similar is true for rational expressions.  Thus, when dealing with rational expressions we will always suppose that whatever x is it won't give division by zero. Rarely do we write this limitation down, however we will always need to keep them in mind.

For the first one listed we have to ignore x = 1 .  The second rational expression is never being zero in the denominator and thus we don't have to worry regarding any restrictions.  Note down that the numerator of the second rational expression will be zero.  That is okay, we only need to ignore division by zero.  For the third rational expression we will have to avoid m = 3 and m =-2 .

The final rational expression shown above will never be zero in the denominator thus again we don't require having any restrictions.

The first topic which we have to discuss here is decreasing a rational expression to lowest terms. A rational expression has been decreased to lowest terms if all common factors from the numerator & denominator have been canceled out.  Already we know how to do this with number fractions so let's take a rapid look at an example. not reduced to lowest terms

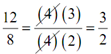                                               ⇒           ⇐    reduced to lowest terms

With rational expression it works accurately the similar way.

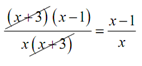
not reduced to lowest terms ⇒

                                 ⇐ reduced to lowest terms

However, we do need to be careful with canceling. There are little common mistakes that students frequently make with these problems.  Remind that to cancel a factor it has to multiply the whole numerator and the whole denominator.  Thus, the x+3 above could cancel as it multiplied the whole numerator & the whole denominator.  Though, the x's in the decreased form can't cancel as the x in the numerator is not times the whole numerator.

To see why the x's don't cancel out in the reduced form above put a number in & see what takes place. Let's plug in x=4.

Obviously the two aren't the similar number!

Thus, be careful with canceling out.  Since a general rule of thumb remember that you can't cancel out something if it's got a "+" or a "-" on one side of it. There is one exception of this rule "-" that we'll deal along with in an example later on down the road.