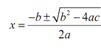Quadratic Formula

It is the final method for solving quadratic equations & it will always work.  Not only that, although if you can recall the formula it's a fairly simple procedure as well.

We can derive the quadratic formula through completing the square on the general quadratic formula in standard form.  Let's do that and we'll take it sort of slow to ensure all the steps are clear.

First, as already noted we ought to have the quadratic equation in standard form.  Next, we have to divide both sides by a to obtain a coefficient of one on the x² term.

ax² + bx + c= 0

x² +( b/ a) x +(c /a)= 0

After that, move the constant to the right side of the equation.

                             x² + (b/a) x =  -  c/ a          

Now, we have to calculate the number we'll have to complete the square.  Again, it is one-half the coefficient of x, squared.

                                (b /2a) ²= b² /4a²

Now, add this to both of the sides, complete the square & get common denominators on the right side to simplify things up a little.

x² + (b/a) x +b²/4a²  =b²/4a²  -(c/a)

(x+(b/2a))² = b²-4ac/4a²

Now we may employ the square root property on this.

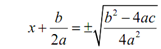
Solve out for x & we'll also simplify the square root a little.

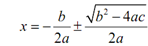
As a final step we will notice that we've got common denominators on the two terms and thus we'll add them up.  Doing this gives,

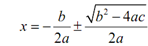
Thus, summarizing up, provided that we begin in standard form,

                      ax² +bx + c = 0

and that's very significant, then the solution to any quadratic equation is,