This problem familiarizes you with using random numbers in C++. The program is to compute a good approximation of π using a simulation method called "Monte Carlo". The following figure shows a circle of radius 1, centered at the origin and circumscribed by a square.

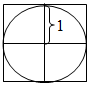
Imagine that this is a dartboard and that you are tossing darts at it randomly. With enough darts, the ratio of darts in the circle (N_c) to total darts thrown (N_t) is approximately equal the ratio between the area of the circle (circle_area = π(1)²) and the area of the square (square_area = 4) i.e.

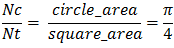
Therefore, 4N_c/N_t . We can simplify the math by only considering the first quadrant, calculating the ratio of the number of darts landed on the first quadrant over the number of darts landed on the top right square's area.

Study the following link to learn how to assign a random number to a variable. Define variables to store the x and y coordinates of a particular dart throw. In other words a random number between [0,1] gets assigned to the variables x and y, each (simulating one dart throw). Now, place your x and y declarations in a For-loop to simulate N dart throws. Note that all of these darts land on the top right square.

Use the Euclidean distance formula,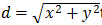 to check if a dart is landed inside the first quadrant. Maintain account of the number of darts that end up in the first quadrant of the unit circle.

Now use your loop to build a π-calculating function. The function should take one argument specifying the number of dart throws to run. It should return the decimal value of π, using the technique outlined above. You should get pretty good results for around 5,000,000 dart throws! Isn't this neat?