Problems on Cantilever Truss:
In the case of cantilever trusses, it is not required to determine the support reactions. The forces in members of cantilever truss are obtained by begning the calculations from free end of cantilever.
Q Determine forces in all the member of cantilever truss shown in the figure given below
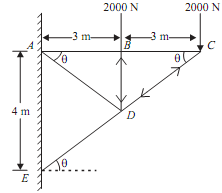
Sol.: From ?ACE, we have
tan θ = AE/AC = 4/6 = 0.66 ...(i)
Also, 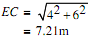
cos θ = AC/EC = 6/7.21 = 0.8321 ... (iii)
sin θ = AE/CE = 4/7.21 = 0.5548
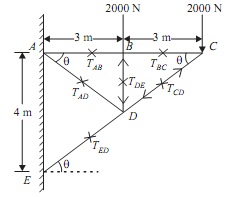
Joint C:
Consider free body diagram of joint C as shown in the given figure;
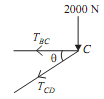
As the three forces are acting, so apply lami's theorem at the joint C.
TBC/sin(90 - θ) = TCD/sin270 = 2000/sin θ
TBC/cos θ = TCD/sin 270 = 2000/sin θ
TBC = 2000/tan θ = 2000/0.66 = 3000.3N ...(v)
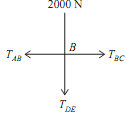
Joint B:
TBC = 3000.3N (Tensile) .......ANS
TCD = - 2000/sin θ = 2000/0.55 = 3604.9N ...(vi)
TCD = 3604.9N (Compressive) .......ANS
Consider free body diagram of joint B as shown in the given figure
As, TBC = 3000.3N
Let, TAB = Force in the member AB
TDB = Force in member DB
As the four forces are acting at the joint B, So apply resolution of forces at joint B
RH = TAB - TBC = 0, TAB = TBC = 3000.03 = TAB
TAB = 3000.03 ...(vii)
TAB = 3000.03N (Tensile) .......ANS
RV = - TDB - 2000 = 0
TDB = -2000N ...(viii)
TDB = 2000N (compressive) .......ANS
Joint D:
Consider free body diagram of joint D as shown in figure given below
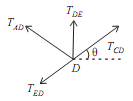
As, TDB = - 2000N
TCD = 3604.9N
Let, TAD = Force in member AD
TDE = Force in member DE
As the four forces are acting at the joint D, So apply resolution of forces at
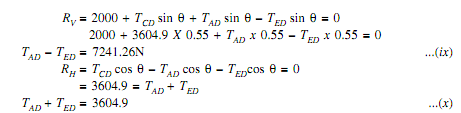
By solving equation (ix) and (x),
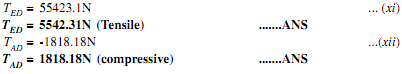
|
Member
|
AB
|
BC
|
CD
|
DE
|
DB
|
AD
|
|
Force in N
|
3000.03
|
3000.03
|
3604.9
|
5542.31
|
2000
|
1818.18
|
|
Nature
C = Compression
T = Tension
|
T
|
T
|
C
|
T
|
C
|
C
|