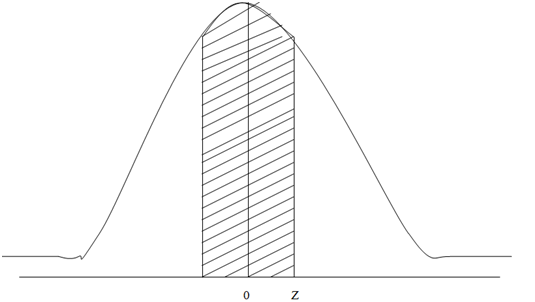
Probability Distribution for Continuous Random Variables

In a continuous distribution, the variable can take any value within a specified range, e.g. 2.21 or 1.64 compared to the specific values taken by a discrete variable e.g 1 or 3. The probability is represented by the area under the probability density curve between the given values.

The uniform distribution, the normal probability distribution and the exponential distribution are examples of a continuous distribution

-           The normal distribution is a probability distribution which is used to determine probabilities of continuous variables

Examples of continuous variables are

• Times
• Capacity Heights
• Weights
• Distances
• e.t.c

- Generally continuous variables are those that can be measured by utilizing the suitable units of measurement.

- specified are the properties of the general distribution

1. The sum of area under the curve is = 1 which is equivalent to the maximum value of probability

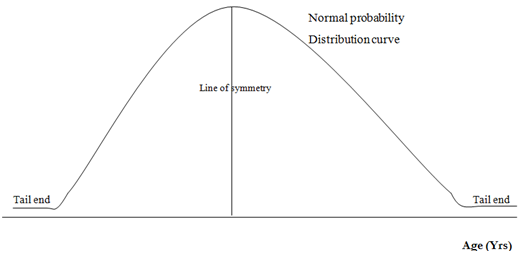
2. The line of symmetry divides curve into two equal halves

3. The two ends of the general distribution curve continuously approach the horizontal axis however they never cross it

4. The values of the mean, mode and median all each are equal

NB: The above distribution curve is referred to as general probability distribution curve since if a frequency distribution curve is plotted from measurements of a specified sample drawn from a general population then a graph similar to the normal curve must be acquired.

- It should be noted that 68 percent of any population lies in one standard deviation, ±1σ

- 95 percent lies in two standard deviations ±2σ

- 99 percent lies in three standard deviations ±3σ

Whereas σ = standard deviation