Examining the Population Variance

Business decision making does not limit itself to setting up the hypothesis to test for the equality of more than two means or proportions simultaneously. This may be attributed to the everchanging and dynamic economic environment. It throws up situations wherein, the managers not only have to deal with the means and proportions but also have to objectively look at and probe the extent as well as the magnitude of the variability present in the population, determine the accuracy of the estimate and the degree of uncertainty that can be associated with such estimates.

In this part of the chapter, first we will look at the distribution of the sample variance for a population and conclude this chapter after looking at the distribution for the sample variance of two populations.

Inference about a Population Variance

Since it is difficult to collect information about the population in an exhaustive manner, we employ the sample variance (s²) as an estimate for the population variance (s²). The square root of s² and s² gives us the standard deviation of the sample and the population. But to calculate the limits, we require a sampling distribution. If the population variance s², exhibits the characteristics of a normal distribution then the corresponding statistic is better described by a Chi Square distribution with n - 1 degrees of freedom. The Chi Square statistic for a sample variance is given by

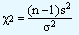......(1)

It is then possible to use Chi Square distribution to arrive at the confidence intervals for the parameter s². Since the confidence intervals and the testing of the hypothesis is about s² the population variance, equation (1) can be rewritten as   

This facilitates us to find the confidence intervals for s². The lower and the upper confidence intervals are given by

 

Figure

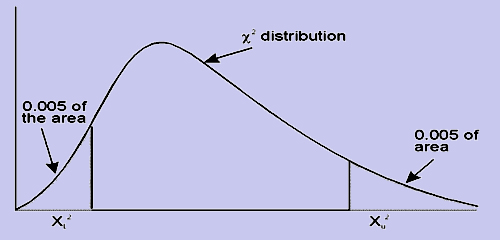
Since we know the values of   , the square root of these two will give us the confidence interval for the standard deviation.

Posted Date: 9/15/2012 6:26:34 AM | Location : United States

Ask an Expert

Related Discussions:- Population variance, Assignment Help, Ask Question on Population variance, Get Answer, Expert's Help, Population variance Discussions

Write discussion on Population variance
Your posts are moderated

Write your message here..

Related Questions

Markov Chain, Each weekend, Derek either reads a book (B), goes to the cine... Each weekend, Derek either reads a book (B), goes to the cinema (C), visits his local museum (M), or plays squash (S). If he reads a book one weekend, then he will take part in one

Weight distribution, What does the confidence level of a confidence interva... What does the confidence level of a confidence interval tell you? Suppose that a population has mean, µ, and standard deviation, σ.  What does the central limit theorem tell us

Types of business forecasting , Types  of business forecasting  are genera... Types  of business forecasting  are generally as follows: 1.      Sales  and Demand  forecasts 2.      Porduction  forecasts. 3.       Cost  Forecasts 4.       Financi

Techniques, Q. 1 a) Describe the important quantitative techniques used in ... Q. 1 a) Describe the important quantitative techniques used in public system management. (10) b) Do you think the day will come when all decisions are made with the assistance of

E-mail messages should be answered quickly, Do people of different age grou... Do people of different age groups differ in their response to e-mail messages? A survey by the Cent of the Digital Future of the University of Southern California reported that 70.

Team Collaboration: Business Decision Making Project, Collect data about th... Collect data about the chosen business problem or opportunity at the company. Explain how you obtained a suitable sample of either qualitative or quantitative data. Review data f

Stratified sampling, Stratified Sampling Stratified Sampling is ... Stratified Sampling Stratified Sampling is generally used when the population is heterogeneous. In this case, the population is first subdivided into several parts (or s

Evaluate central tendency and variability, Why are graphs and tables useful... Why are graphs and tables useful when examining data? A researcher is comparing two middle school 7th grade classes. One class at one school has participated in an arts program

Types of sampling, Given a certain population there are various ways in whi... Given a certain population there are various ways in which a sample may be drawn from it. The chart below illustrates this point: Figure 1 In  Judgem

Median for grouped data, Grouped Data  In order to find the median, the... Grouped Data  In order to find the median, the median class is to be first located and then interpolation is to be used by assuming that items are evenly spaced over the entire