Polynomials

In this section we will discuss about polynomials.  We will begin with polynomials in one variable.

Polynomials in one variable

Polynomials in one variable are algebraic expressions which contain terms in the form axⁿ  where n refer to a non-negative (that means positive or zero) integer and a refer to a real number and is termed as the coefficient of the term.  The degree of a polynomial in one variable is the biggest exponent in the polynomial.

Note that we will frequently drop the "in one variable" part and only say polynomial. Here are instance of polynomials and their degrees.

5x¹² - 2x⁶ + x⁵ -198x + 1                                                          degree : 12

x⁴ - x³ + x² - x + 1                                                                    degree : 4

56x²³                                                                                        degree : 23

5x - 7                                                                                       degree : 1

-8                                                                                              degree : 0

Thus, a polynomial doesn't have to contain all powers of x . Also, polynomials can contain a single term.

Here are some instances that aren't polynomials.

4x⁶ + 15x^-8 +1

5 √ x - x+ x²

2/x +x³ -2 = 2x^-1+x³-2

The first one isn't polynomial as it has a negative exponent and all exponents in a polynomial must be positive.

To illustrate why the second one isn't a polynomial rewrite it a little.

                               5 √ x - x+ x² = 5x^1/2-x+x²

By changing the root to exponent form we illustrates that there is rational root in the algebraic expression.  In the algebraic expression all of the exponents have to be integers in order for the algebraic expression to be a polynomial.  As a general rule of thumb if an algebraic expression contain a radical in it then it isn't polynomial.

Let's rewrite the third equation to see why it isn't polynomial.

2/x +x³ -2 = 2x^-1+x³-2

Thus, this algebraic expression really contains a negative exponent in it and it isn't allowed.  Another rule of thumb is if there are variables in the denominator of a fraction then the algebraic expression isn't a polynomial.

Another rule of thumb is if there are any variables in denominator of fraction then the algebraic expression isn't a polynomial.

Notice that it doesn't mean that radicals and fractions aren't let in polynomials. They only can't involve the variables. For example, the following is a polynomial

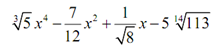
There are many radicals & fractions in this algebraic expression, however the denominators of the fractions are only numbers and the radicands of each radical are only a numbers. In the algebraic expression each x appears into the numerator and the exponent is a positive (or zero) integer. Hence this is a polynomial.