Polynomial Functions

Dividing Polynomials

We're going to discussed about dividing polynomials.

Let's do a quick instance to remind how long division of polynomials works.

Example Divide 5x³ - x² = 6 by x - 4 .

Solution

Let's primary get the problem set up.

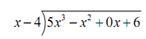
Recall that we have to have the terms written down along the exponents in decreasing order and to ensure we don't commit any mistakes we add in any missing terms  along with a zero coefficient.

Now we need to find what we have to multiply x - 4 to obatin the first term in first polynomial.  In this case that is 5x² .  Hence multiply x - 4 by 5x² & subtract the results from the first polynomial

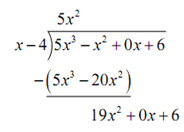
The new polynomial is called the remainder. We carry on the procedure till the degree of the remainder is less than the degree of the divisor, i.e. x - 4 in this case. Hence, we have to continue till the degree of the remainder is less than 1.

Remember that the degree of a polynomial is the highest exponent in the polynomial. Also, recall that constant is thought of as polynomial of degree zero. Thus, we'll have to continue till we get a constant in this case.

Following is the rest of the work for this example.

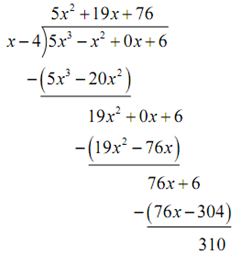
Now that we've gotten this done, let's keep in mind how we write the actual answer down. The answer is,

 5x³ - x² + 6/ x - 4=  5x² + 19x +76 + 310/ x - 4

Actually there is another way to write the answer that we're going to determine much more useful, if for no other cause that it's easier to write down.  If we multiply both sides of the answer by x - 4 we obtain,

                        5x³ - x² + 6 = ( x - 4) (5x²  + 19 x + 76) = 310

In this instance we divided the polynomial through a linear polynomial in the form of x - r and we will be limiting ourselves to only these sorts of problems.  Long division works for much more general division.