Model without Stock Effects

In this model it is assumed that extraction cost depends only on extracted quantity. Let us assume that S_t  is the remaining stock of natural resource at time t, E_t is the quantity  of extraction,  P_t  is  the price at which it is sold  in  the market, r is  the discount rate and C(E_t) is the total cost of extraction. The problem before us is

Equation 1

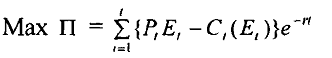
Here we consider the time period t = 1 .... T.

Total profit is ∏, which is the sum of 'revenues minus costs' during all time periods under consideration.

When we extract E_t in time period’t’ there is depletion to the stock. Therefore,

Equation 2

S_t = S_t-1- E_t for all t.

In addition, final stock that remains cannot be negative. Thus, we impose the constraint

S_T  > 0

The Lagrangian function for the above problem is given by

Equation 3

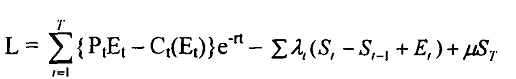
On solving equation 3 the first order condition yields

Equation 4

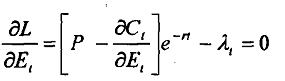
As you know Quantitative Methods, λ, in equation 4 is the present value of the shadow price or opportunity cost, and

Equation 5

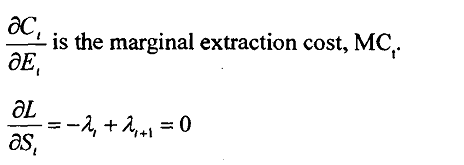
Equation 6

An implication of the first order condition equation 5 is that λ_t = λ_t=1 for all t, which means the present value  of  shadow price  is constant over time, or it  is time independent.

Let us denote 'resource rent' or royalty to be paid as R_t which is given by

R_t= P_t - MC_t = λ_te^rt from the first order condition.

It can be easily shown that

Equation 7

R_t = λ_te^rt  and R_t / R_t = r

Where dot over a variable represents its derivative, i.e., instantaneous change  in it. Thus R denotes the change in R, i.e., resource  rent. From equation 7 we find that resource rent rises at the rate ‘r’.  The resource rent  is equivalent to the present value of opportunity cost. Hence, the present value of opportunity cost rises at  the rate equal to market rate of interest (which we had taken as our discount rate).

The model presented at equation 1 can be expressed using discreet time variable.

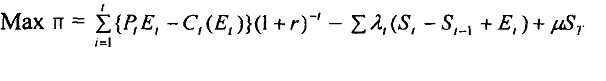
The first order condition would yield

Equation 8

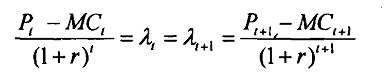
By rearranging terms in equation 8 it is easy to show that

Equation 9

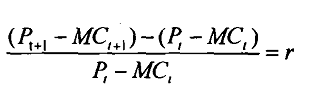
This yields the same  result that the resource rent increases at  the rate 'r'  over  time.  Moreover,

Equation 10

P_t =MC_t + λ_t (1+r)^t

Equation 10 shows that optimal extraction rate is  the one at which the sum of marginal cost and the current value opportunity cost is equal to price.

μ = λ_T = constant              If  S_T >  0  then λ=  0

If  S_T =  0  then λ >  0

Opportunity cost is positive only if the resource stock is completely exhausted within the time horizon.

The following results are popularly known as Hotelling's Lemma.

(i)  Current value opportunity cost increases at the constant rate 'r' equal to market rate of interest.

(ii)  Present value of opportunity cost is constant over time.