The maximum stress in each material:

A copper tube of external diameter 60 mm and internal diameter 40 mm is closely fitted to a steel rod of 40 mm diameter to compose a composite shaft. If a torque of 6 kN-m is to be resisted by the shaft, discover the maximum stress in each material and the angle of twist in 2 m length.

Take  G = 80 kN/mm for steel, and

G = 40 kN/mm² for copper.

Solution

Copper Tube

G = 40 kN/mm²  = 0.4 × 1011 N/m2 , l = 2 m

d₁ = 60 mm = 0.06 m

d₂ = 40 mm = 0.04 m

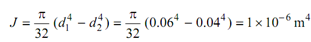
TC = torque resisted by copper tube

θ= Tl/ GJ    =  (TC ) (2) /((0.4 × 10¹¹ ) (1 × 10^{- 6} )) = 2 T_C × 10^{- 5} radians       ---------- (1)

τ_max =  (T/J )× R = (1 × 10^{- 6} ) × (0.03) = 0.03 TC  × 10  N/m

         = 0.03 T_C N/mm²                             ------------ (2)

Figure

G = 80 kN/mm²  = 0.8 × 10¹¹ N/m² ,   l = 2 m

d = 40 mm

J =  (π/32) d ⁴ = (π /32)× 0.044  = 2.5 × 10^{- 7} m⁴

R = 20 mm = 0.02 m

θ= Tl  / GJ  = (T_S ) (2) / ((0.8 × 10¹¹ ) (2.5 × 10^{- 7} )) = T_S × 10^{- 4} radians  --------- (3)

τ_max =(T/ J) × R =  Ts / ((2.5 × 10- 7 ) (0.02)) = 0.008 T_S  × 10⁷  N/m

= 0.08 T_S N/mm²                                    --------- (4)

In composite shafts, θ_C = θ_S

 ⇒        5 T_C  × 10^{- 5}  = T_S  × 10^{- 4}

∴          T_C  = 2T_S                                  -------- (5)

T_S  + T_C  = T

⇒         T_S = 2T_S  = 6

∴          T_S = 2 kN-m             T_C  = 4 kN-m

∴ Angle of twist, θ= (2 × 10³ ) × 10^{- 4}  = 0.2 radians

Maximum Shear Stress

For copper shaft : For steel shaft :

τ_max  = 0.03 × 4 × 10³  = 120 N/m²

τ_max  = 0.08 × 2 × 10³  = 160 N/m²