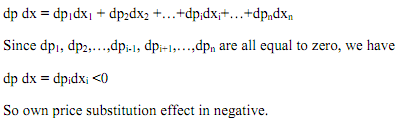Mathematical Derivation of ordinary demand function:
Here we present the mathematical and more general proof of the above result. Consider, again, the initial price income situation (p0, M0), where x0 is the chosen bundle. Prices change from p0 to p1, where p0>p1, and consumer's real income changes (in this case increases). Suppose we adjust consumer's money income in such a way that her purchasing power remains the same. Consumer's money income is changed to M1 = p1x0. Suppose x" is the bundle consumer buys with her adjusted money income viz.,
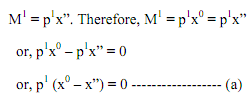
Since with (p1, M1) consumer chooses x" while x0 was available, so x" is revealed preferred to x0 and therefore was not available when x0 was chosen while (p0, M0) prevailed. Thus,
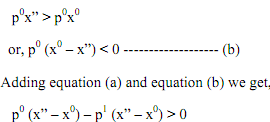
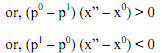
Suppose only price of ith good changes, other prices remaining constant. Therefore,
(pi0 - pi1) (xi" - xi0) < 0
So, quantity change is in opposite direction of the price change. Hence, substitution effect is negative. Now, dp = (dp1, dp2,...,dpi,...,dpn) and dx = (dx1, dx2,...,dxi,...,dxn)T, so that