Q. Explain Linear Regression model?

Ans.

Linear correlation measures the strength of a linear relationship, but not the exact numerical relationship. Linear regression, on the other hand, helps us predict outcomes given a data set. For example, how can we predict the distance needed by a car to stop based on its speed?

Given the value of an independent variable (x-axis), we want to be able to predict the value of the dependent variable (y-axis).

In order to make these predictions, we use the linear-regression line or the least-squares line with the scatter plot of data.

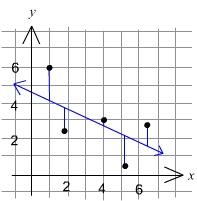
The linear-regression line fit minimizes the vertical distances for a data set. (See the vertical blue lines in the diagram).

In fact, the closer the correlation coefficient, r, is to +1 or 1, the better the linear-regression line fits the data. Recall that when r = +1 or 1 the data is said to have a perfect correlation (all points of the data set will lie on a line). The linear-regression line can be found using a graphing calculator. There are more sophisticated methods of finding the linear-regression line that are taught in more advanced statistics courses.

Statisticians look for the equation of the linear-regression line because it expresses the relationship between the two variables x and y. Regression analysis calculates an equation that provides values of y for given values of x. Usually the exact value of y is not predictable, but regression analysis will allow us to make reasonably close predictions.