Limits

The concept of a limit is fundamental in calculus. Often, we are interested to know the behavior of f(x) as the independent variable x approaches some particular point 'a'. The question is, if we give values to x which are nearer and nearer to 'a', will the values of f(x) come nearer and nearer to any particular value? Suppose we define a function f(x) as:

                            f(x) = 2x

It can be seen that as we give values to x which are nearer and nearer to 0, then the value of f(x) also comes nearer and nearer to 0.

If x approaches a value 'a', f(x) approaches some number L, then we say that the limit of f(x) approaches L. This is symbolically written as

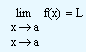        is to be read as 'x approaches a'.

Sometimes we may allow x to take values which are larger and larger, without any limit. This is symbolically written as 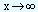  (read as 'x approaches infinity'). If f(x) approaches a limit L as  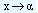 , then we write

In some cases, it may so happen that as x approaches a value, the value of the function f(x) may become larger and larger without any limit. This is symbolically written as:

Example 

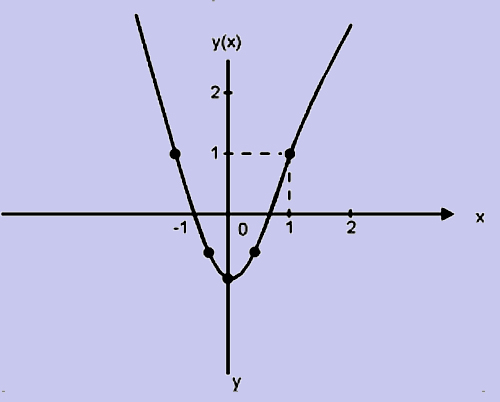
Suppose f(x) = 2x² - 1

As x approaches value 1, f(x) approaches the value 1,

This is graphically represented below.

Figure