ladder slip:

A uniform ladder having length of 7m rests against vertical wall with which it makes an angle of 45º, coefficient of friction between ladder and wall is 0.4 and that between ladder and the floor is 0.5. If a man having weight is one half of that of ladder, ascends it, how high will it be when ladder slips?

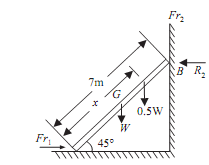
Sol.: Let,

X = Distance between A and man, when ladder is at point of slipping.

W = Weight of ladder

Weight of man = W/2 = 0.5W

Fr₁ = 0.5R₁                                 ...(i)

Fr₂ = 0.4R₂                                 ...(ii)

Resolving forces vertically

R₁  + Fr₂  - W - 0.5W = 0

R₁  + 0.4R2 = 1.5W                       ...(iii)

Resolving forces Horizontally

R₂  - Fr₁ = 0; R₂  = 0.5R₁                                   ...(iv)

By solving equation (iii) and (iv), we get

R₂ = 0.625W, Fr₂  = 0.25W

Now taking moment about the point A,

W × 3.5cos45° + 0.5W × xcos45° - R₂  × 7sin45° - Fr₂  × 7cos45°

By putting the value of R₂  and Fr₂, we get

X = 5.25m                                                    .......ANS