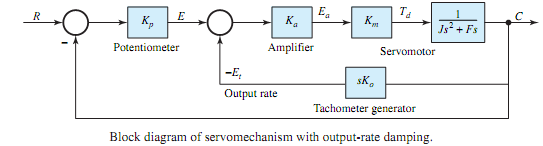
Q. Illustrate Output-rate control?
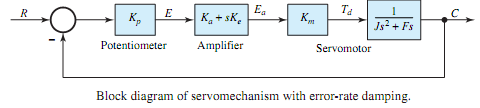
A system is said to have output-rate damping when the generation of the output quantity in some way ismade to depend upon the rate atwhich the controlled variable is varying.Output-rate control often involves the creation of an auxiliary loop, making the system multiloop. For the system of Figure, output-rate damping can be obtained by means of a tachometer generator, driven from the servomotor shaft. The complete block diagram of the servomechanism with output-rate damping is depicted in Figure, where Ko is the output-rate gain factor (V·s/rad) and the output-rate signal is given by Ko(dc/dt). By applying the feedback relationship of Equation to the minor (inner) loop, one gets
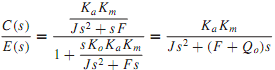
where Qo = KoKaKm is known as the loop output-rate gain factor. Figure may then be simplified. The closed-loop transfer function for the complete system is then given by
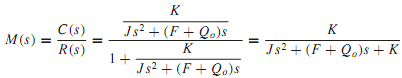
where K = KpKaKm is known as the loop proportional gain factor, as stated earlier.
The manner in which output-rate damping effects in controlling the transient response are most easily demonstrated is by assuming a step input applied to the system. The output-rate signal appears in opposition to the proportional signal, thereby removing the tendency for an excessively oscillatory response.With error-rate damping and output-rate damping, the damping ratio can be seen to be
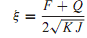
where Q = Qe or Qo, in which a term is added to the numerator, while the natural frequency is unchanged (as given by ωn = √K/J ). The damping ratio can then be adjusted independently through Qe or Qo, while K can be used to meet accuracy requirements.