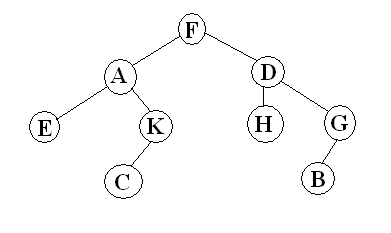
Q. A Binary tree comprises 9 nodes. The preorder and inorder traversals of the tree yield the given sequence of nodes:

Inorder :          E     A    C    K    F     H    D    B    G

Preorder:         F     A    E    K    C    D    H    G    B

Draw the particular tree. Explain your algorithm as well.

Ans.

Inorder:        E     A     C     K     F     H     D     B     G

Preorder:     F     A     E     K     C     D     H     G     B

The tree T is drawn from its root downward as shown below.

a)      The root T is obtained by selecting the first node in its preorder. Therefore, F is the root of T.

b)      The left child of the node F is obtained as shown here. First use the inorder of T to find the nodes the in the left subtree T1 of F. Thus T1 consists of the nodes E, A, C and K. Then the left child of F is obtained by choosing the first node in the preorder of T1 (which appears in the preorder of T). Therefore A is the left son of F.

c)     Likewise, the right subtree T2 of F comprises of the nodes H, D, B and G, and D is the root of T2, that is, D is the right child of F.

Performing the above process with each new node, we finally obtain the desired tree.