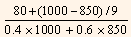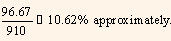Illustration

Consider a Rs.1,000 par value bond whose current market price is Rs.850. The bond carries a coupon rate of 8% and has a maturity period of 9 years. What would be the rate of return that an investor earns if he purchases the bond and holds till maturity?

Solution

The rate of return earned, also referred to as yield to maturity, is the value of k_d in the following equation:

         P₀               =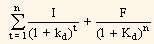     

         Rs.850          =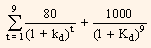     

                            =     Rs.80 (PVIFA_{kd%, 9 yrs}) + Rs.1,000 (PVIF_{kd%, 9 yrs.}).

Where,

         I        =   Interest

         F       =   Face value

         k_d      =   Cost of debt

         P₀      =   Current market price.

To find out the value of k_d in the above equation, several values of k_d will have to be tried out in order to reach the input value. Therefore, to start with, consider a discount rate of 12% for k_d for which the expression becomes equal to:

         = Rs.80 (PVIFA _{12%, 9 yrs}) + Rs.1,000(PVIF_{12%, 9 yrs.})

         = Rs.80 x 5.328 + Rs.1,000(0.361)

         = Rs.426.24 + Rs.361 = Rs.787.24.

Since the above, value is less than the market price, we have to try with a less discounting rate (k_d). So, let k_d = 10%, then the equation becomes:

         = Rs.80(PVIFA_{10%, 9 yrs.}) + Rs.1,000 (PVIF_{10%, 9 yrs.})

         = Rs.80 x 5.759 + Rs.1,000 x 0.424

         = Rs.460.24 + Rs.424 = Rs.884.72

From the above, it is clear that k_d lies between 10% and 12%. Now, we have to use linear interpolation in the range of 10% and 12%. k_d is determined as follows:

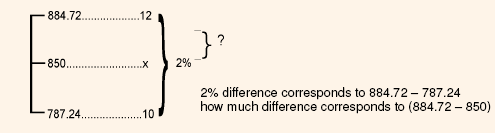
                        = 10% + (12 - 10%)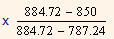      

                   = 10% + 2%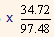 

                   = 10% + 2% x 0.356

                   = 10% + 0.71

                   = 10.71%

The yield to maturity is 10.71%.

An Approximation: As trial and error methods of calculation are tedious, the following approximation formula can be employed to find out the approximate YTM on a bond.

         YTM =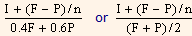        

Where,

           YTM          =     Yield to maturity.

                   I       =     Annual interest payment.

                   F       =     Par value or redemption value of the bond.

                   P       =     Current market price of the bond.

                   N       =     Years to maturity.

Therefore,

         YTM =