Games with Strategic Moves

The ideas in this chapters can be brought to life and the students can better appreciate the subtleties of various strategic moves and their credibility if you hold classroom discussions based on situations where such strategies are of the essence. Depending on your preference, you can either have the discussion before any formal analysis is done and develop the analytical concepts and techniques out of the ideas that arise during the discussion, or the other way around. Similarly, because brinkmanship is critically linked to the issues covered.

We have found that students have the most difficulty grasp- ing the distinction between deterrence and compellence. It is often especially hard for them to identify the four possible types of threats and promises and the circumstances in which the various combinations can best be used. You may want to take the time to construct specific examples of each type of threat and of scenarios in which each is most likely to be used. We emphasize two points: (1) deterrent threats and com- pellent promises are the most common conditional response rules, and (2) compellent threats and deterrent promises re- quire that the player making the strategic move impose some type of time limit on the rival. In discussion with the class, students usually connect the fact that point 2 helps explain why point 1 holds.

To convey the basic ideas of commitments, threats, and promises using examples or here are some other possible examples.

For a commitment example, you can return to the Battle- of-the-sexes" example; the game was between a husband and wife trying to decide on a film to see, Independence Day or The English Patient. The payoff matrix is as follows:

This game has two Nash equilibria in pure strategies (and one in mixed strategies). Either player in this game could use a strategic move to better his or her expected equilibrium payoff. By restricting her own freedom of action, for instance, the wife could commit to seeing The English Patient; she could do so by spending her last $8 on a ticket for that film. Or the wife could take some action that changed the payoffs in the game, changing her payoff from seeing Independence Day with her husband to -1 instead of 1; perhaps his be- havior during such films makes it even worse for her to see them with him rather than without him. In either case, the unique Nash equilibrium of the game becomes (The English Patient, The English Patient).

You can then cover the standard practical difficulties that one must consider with commitment moves. The other player (the husband here) may not receive the necessary informa- tion about your commitment move; this may be a deliberate move on the other player's part. In addition, the other player may not believe your commitment (brings up issues of cred- ibility). Finally, simultaneously clashing commitments may lead to a bad outcome.

For a different example of a game in which a threat can alter the outcome to a player's benefit, consider a sequential game between you and a mugger: you make the first move and decide whether to give up your wallet; then the mugger decides whether to stab you. The tree for this game in its original (no strategic move) format is illustrated below.

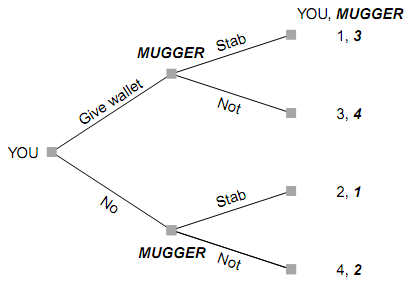
The Nash equilibrium with no strategic moves shows that no stabbing is a dominant strategy for the mugger; given this, you choose not to give up your wallet. The payoffs in equi- librium to you and the mugger are (4, 2). You get your high- est possible payoff and can do nothing to improve your payoff in this game, but the mugger can make a threat to change the path of play and improve his outcome.

The mugger can use a threat: "If you don't give me your wallet, then I will stab you." This is a compellent threat with an implicit promise that you will not be stabbed if you do hand over your wallet. If you believe the threat, then it is in your interest to give up your wallet (and get a payoff of 3) rather than not (and get a payoff of 2). Of course, it is not optimal for the mugger to carry out the threat if put to the test (mugger gets 1 instead of 2 if he follows through due to the risk of a felony conviction and a long prison term), so credibility is problematic. The mugger could establish credibility in this case through irrationality-acting crazy and out of control.

For an example of a promise, you can use a variant on the parent-child game. This sequential game is illustrated in the tree below. Payoffs assume that the Child

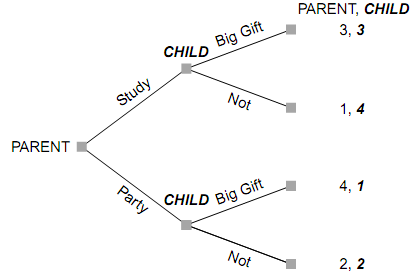
prefers outcomes with a Big Gift over those without a gift and then prefers to Party rather than Study; the Parent wants the Child to Study above all and then prefers outcomes in which no gift is necessary. The Nash equilibrium shows that the parent chooses No regardless of the child's choice, so the child chooses Party rather than Study. The payoffs are 2 to the child and 2 to the parent.

The Parent can improve his outcome-and get the child to Study-by using a compellent promise: "If you study, I will give you a big gift." The implicit threat here is that there is no big gift if the child parties; this is automatically credible given the payoff structure of the game. Credibility of the promise is questionable because purchasing the big gift is not in the parent's best interest once the child has done the studying. The parent can establish credibility of such a promise with a reputation for following through; this works especially well for younger siblings.

Finally, for an example of a game which requires both a threat and a promise, consider this example about the U.S. House of Representatives vote on Reagan's 1981 tax cut bill. The payoff table for the game between the Democrats in the House and the Republicans in the House is as follows:

The payoff structure depends on the following considerations related to the various outcomes. In the (Weak Opposition, Hard-Line Support) cell, there is a Republican victory and the Democrats maintain the ability to say, "Don't blame us." In the (Weak Opposition, Compromise) cell, the Republicans win but not totally; Reagan is unhappy and the Democrats get to share the credit. In the (Hard-Line Attack, Hard-Line Support) cell, Reagan's program is blocked in the House and the Democrats get the blame for thwarting a popular president. Finally, in the (Hard-Line Attack, Compromise) cell, the Republicans lose much of their program and the Democrats look fiscally responsible.

The Nash equilibrium of the game without strategic moves entails Weak Opposition by the Democrats and Hard-Line Support by the Republicans; payoffs are (2, 4). The Demo- crats have an incentive to use a strategic move to better their outcome. They could try to use a commitment move, but committing to Hard-Line attack leaves them with a payoff of 1 instead of the 2 they get with Weak Opposition, so a commitment does not help. Instead they must consider a threat and/or a promise.

For a threat, the Democrats would want to say, "If you give Hard-Line Support, we will offer Hard-Line Attack." This is not immediately credible since Hard-Line Attack is not in the Democrats best interest if the Republicans offer Hard-Line Support. Similarly, the implicit promise that goes along with this threat-"If you compromise, so will we"- is not credible since Weak Opposition is not the choice the Democrats would want to make against compromising Repub- licans. (If the Democrats wanted to make just the promise, they would find that its implicit threat was not credible.) The Democrats must use a combination of a threat and a promise, explicitly stating both parts of the response rule: "We will match compromise for compromise, hard line for hard line." Both parts need to be made credible as well, potentially through the establishment of a reputation in the ongoing (re- peated) game between House Republicans and Democrats. In reality, this did not happen.

You may find it useful to come up with your own, per- haps university-specific, examples of methods by which players can enhance the credibility of their strategic moves. For universities with an honor code, the credibility of such a code can provide an excellent discussion topic for this chapter. Also, the text discusses how "apparently irrational motives like honor or face" may make it credible that you will deliver on a promise. One possible example of this is the tradition of the U.S. Marines never to leave any of their dead behind on the field of battle; inculcating this philos- ophy into all Marines may make credible a great deal of trust between soldiers.

As for the discussion topics we mentioned earlier, there are three different scenarios that we have used in order to stimulate class discussions. The first concerns governments' negotiations with terrorists who are holding hostages. We consider the typical situations in which such negotiations arise, the types of policies governments consider, and the cred- ibility issues that arise, as well as the various components of the negotiations themselves.

In the second scenario, we schedule an extended session of the class and screen the movie Dr. Strangelove (which lasts 95 minutes). In the following class session we hold a discussion on the strategic issues that arise in the movie. (Another option is to schedule an evening showing of the film and/or to have students rent the film and see it on their own. Some school libraries may have the film in their col- lection either on VHS or laser disc.) This movie is full of incidents where threats, promises, credibility, and so on, are of the essence. In movie-buffs' polls it is often ranked in the all-time top-10 lists, and it engages the interest of most of our students. But it is in black and white, it lacks modern visual special effects, and its premise of superpower nuclear confrontation is ancient history to many of today's students. If you want to use this film and have the technology avail- able (laser disc would be the easiest), you can bring the film to the discussion class and show critical scenes as they are brought up for discussion.

You can instead use this movie in conjunction; the impact is greater if the class sees it while the drama of the Cuban missile crisis is fresh in their minds.

Of course, many other more recent movies have brief individual scenes where strategic moves are played. You might be able to arouse greater interest in such films than is possible with Dr. Strangelove; if you can put together a video- tape that assembles such scenes from a number of movies, you can get more varied and more modern settings and use these as the basis for your discussion. We have just recently tried to do something like this, digitizing short video clips for students to view and comment on electronically. This procedure allows for an ongoing conversation that continues beyond the bounds of a 50- or 70-minute class period; as an added bonus, you get a record of the conversation using this method.

A third possible topic is the game between political pris- oners and their jailers. The inspiration for this came from reading Nelson Mandela's Long Walk to Freedom, (Boston: Little, Brown, 1994), especially the chapters "Robben Island: The Dark Years" and "Robben Island: Beginning to Hope." This topic proved a good way to get across the point that even though your sympathy is entirely on one side, to understand and analyze the game properly you must also understand the strategies and the objectives of the other side.

For your guidance, we append summaries of our dis- cussions of each of these topics. We do this with a twofold purpose. If you choose one of these topics, these summaries will give you points with which you can lead the discussion in interesting directions if it begins to lag or go off in irrele- vant directions. If you choose some other topic, these sum- maries may suggest general ideas about organizing your own topic ahead of time and being ready to offer pointers to the class. We apologize for the terse and notelike (often ungrammatical) quality of these summaries; a fuller version would be too long.