There may be more than one independent variable which determines the value of y. The dimension of a function is determined by the number of independent variables in the domain of a function. For example:

y = f(x, z) is a two dimensional function.

y = f(x₁, x₂, ....x_n) is an n-dimensional function.

Example 

In capital budgeting, the net present value (y) of an investment project is defined as a function of the net cash flows in different time periods, project's initial cash outlay, the firm's cost of capital, and the life of the project.

This relationship can be expressed functionally as:

                   y      = f(C_t, B, P, N)

where,

                    C­_t    =     net cash flow in time period t (t = 1, 2, ....N)

                   B      =     the project's initial cash outlay

                   P      =     the firm's cost of capital

                   N      =     the life of the project

It is known that this function is:

y  = f(Ct, B, P, N)

=

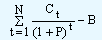For any given values of the right hand side independent variables, we can determine the left hand side dependent variable in a unique manner.

Posted Date: 9/13/2012 5:52:49 AM | Location : United States

Ask an Expert

Related Discussions:- Functions of many variables, Assignment Help, Ask Question on Functions of many variables, Get Answer, Expert's Help, Functions of many variables Discussions

Write discussion on Functions of many variables
Your posts are moderated

Write your message here..

Related Questions

#title.college algebra., -15divided by(-1_-4 -15divided by(-1_-4

Hexagon, how many sides does a regular hexagon have? how many sides does a regular hexagon have?

Permatuation and combination problem, How may six digit numbers can be made... How may six digit numbers can be made in which the sum of the digits is even? Ans = 9*10*10*10*10*5

Profit and loss, A man sold an item for Rs 6,750 at a loss 25%. What will b... A man sold an item for Rs 6,750 at a loss 25%. What will be the selling price of same item if he sells it at a profit of 15%?

Combination, nC6:n-3C3=91:4 nC6:n-3C3=91:4

#title percentage, /100*4500/12 /100*4500/12

The number of filtering steps, The amount of particulate matter left in sol... The amount of particulate matter left in solution during a filtering process is given by the equation p(n) = 500(2) -0.8n , where n is the number of filtering steps. Find the amoun

Dumpy level, Hi there, I am doing a math assignment at current, however I a... Hi there, I am doing a math assignment at current, however I am having trouble with a question about dumpy level, and finding whether the slope of the block will be suitable for th

Properties of logarithms, Properties of Logarithms 1. log a x... Properties of Logarithms 1. log a xy = log a x + log a y 2.  = log a x - log a y 3. log a x n   = n log

Simultaneous equations, Before we look at simultaneous equations let ... Before we look at simultaneous equations let us brush up some of the fundamentals. First, we define what is meant by an equation. It is a statement which indicate