Frictional force acting on the ladder:

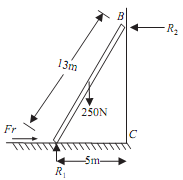
A uniform ladder having length 13m and weighing 250N is placed against smooth vertical wall with its lower end 5m from wall. The coefficient of friction between ladder and floor is 0.3. Show that ladder will remain in equilibrium in the position. What is frictional force acting on the ladder at the point of contact between the ladder and the floor?

Sol.: Since the ladder is placed against a smooth vertical wall, hence there will be no friction at point of contact between the ladder and wall. Resolving all the force vertically and horizontally.

∑H = 0, F_r  - R₂  = 0                   ...(i)

∑V = 0, R₁  - 250                       ...(ii)

From the geometry of the figure, BC = 12m

By taking moment about point B,

R₁  × 5 - F_r  × 12 - 250 × 2.5 = 0

F_r = 52N                                        .......ANS

For equilibrium of ladder, Maximum force of the friction available at point of contact between the ladder and floor = µ_R

= 0.3 × 250  = 75N                    .......ANS                     

Thus we see that amount of force of friction available at point of contact (75N) is more than force of friction required for the equilibrium (52N).  Thus, the ladder will remain in equilibrium in the position.