Question 1- In engineering applications it is often necessary to fit a straight line to a set of N points with known coordinates (xi, yi), where i indexes the points (N in total). Under certain assumptions, the equation of the line-of-best-fit through N points that also passes through the origin is given by

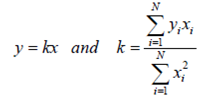
where k is the slope of the line.

Write a subroutine (find_k) that receives the coordinates of N points from a calling program and calculates/returns the coefficient k in the best-fit equation through the origin. The size N of the arrays should be supplied to the subroutine as a separate integer argument.

Test your subroutine by computing the coefficient k for the line that best fits the following points:

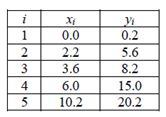
The data should be read from a data file named "points.dat" in the main program. The first line of the file should contain the number of points to be read. The following lines should contain pairs of numbers describing the coordinates of N points (one pair per line).

The arrays (array) storing the coordinates should allocatable. The program should output the value of k computed by the subroutine to the screen, using formatted output with 3 decimal places. Prepare a short report plotting the points and the line of best fit (either using Excel, or any other graphics program). Report the value of k used.

Question 2- A point in a rank-2 array is said to be a relative maximum if it is higher than any of the 8 points surrounding it. For example, the element at position (2,2) in the array shown below is a relative maximum, since it is larger than any of the surrounding points.

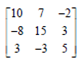
Write a program to read a matrix A from an input file, and to scan for all relative maxima within the matrix. The first line in the file should contain the number of rows (m) and the number of columns (n) in the matrix, and then the next lines should contain the values in the matrix, with all of the values in a given row on a single line of the input file. Use an allocatable array for matrix A. The program should only consider interior points within the matrix, since any point along an edge of the matrix cannot be completely surrounded by 8 points. Your program must output all relative maxima and their locations (number of the row and number of the column where the relative maximum is located) on the screen. Test your program by finding all of the relative maxima of the following matrix, print/report the results.