Formula for maximum power transmitted by belt:

Derive formula for maximum power transmitted by belt when centrifugal tension is considered.

Sol: Let T₁  = Tension on tight side T₂  = Tension on slack side v = Linear velocity of belt

Then the power transmitted can be given by the equation

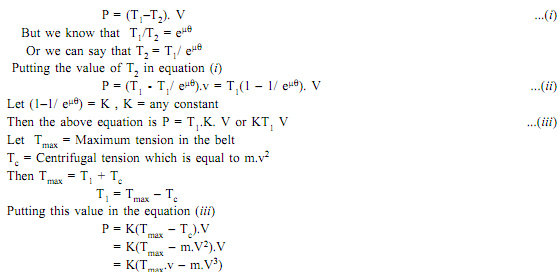
Power transmitted will be maximum if d(P)/dv = 0

Thus differentiating equation with respect to V and equating to zero for maximum power, we get

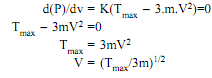
Equation (iv) gives velocity of belt at which maximum power is transmitted.

From equation (iv) T_max  = 3T_c                                                                                                                      ...(v)

Hence when power transmitted is maximum, the centrifugal tension would be around 1/3^rd of the maximum tension.

We know that T_max = T₁  + T_c

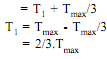
Hence condition for transmission of maximum power is:

T_c = 1/3 T_max, and     

T₁  = 2/3T_max                                                                                                                    ...(viii)

NOTE: The net driving tension in the belt = (T₁  - T₂)