There are several methods available to forecast yield volatility. But before that, let us look into the calculation of forecasted standard deviation.
Assume that a trader wants to forecast volatility at the end of 07/08/2007, by using the 20 most recent days of trading and update the forecast at the end of each trading day. To calculate these, the trader can calculate a 20-day moving average of the daily percentage yield change.
Still now it has been assumed that the moving average is an appropriate value to use for the expected value of the change in yield. But, some experts view that it would be more appropriate to assume the expected value of the change in yield to be zero. In eq. (1) by substituting zeros in place of moving average X, we get
Variance =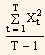 
...Eq (2)
An equal weightage is assigned to all observations by the daily standard deviation given by equation 2. Therefore, a weightage of 20% for each day is given if the trader is calculating volatility based on the most recent 20 days of trading.
Greater weightage is given to recent movements in the yield or price while determining volatility, and less weightage is given to the observations that are farther in the past. Revising equation 2 to include the weightages we get,
Variance =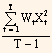 
...Eq. (3)
Wt is the weight assigned to the observations t. The sum of all the weights assigned to the observation will be equal to 1.
A time series characteristic of financial assets suggests that a high volatility period is followed by a high volatility period and a low volatility period is followed by a low volatility period. From this observation, we can tell that the recent past volatility influences current volatility. This time series property of volatility can be estimated with the help of statistical models like autoregressive conditional heteroskedasticity.