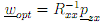Optimal Filtering

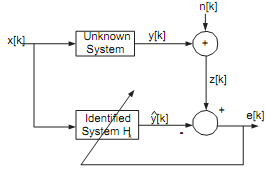
A system identi?cation structure is shown in Figure 1. The discrete-time signal [ ] forms the input to an unknown system represented by a moving average, FIR, ?lter with parameters, {ω₀,ω₁ ω_n} . The output of the unknown system is given by

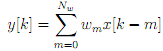
This can be represented more concisely in vector notation as

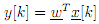
where ω and x[k] are N_w + 1 element column vectors, underlines are used to denote vector quantities and the superscript (·)^T represents a vector transpose.

A noise signal n[k] is added at the output of the system to yield a realistic measured output signal z[k]. An optimum ?lter is to be designed which operates on the input signal x[k] and measured output signal z[k] to yield the closest match to the unknown system. The optimum ?lter is assumed to be a moving average ?lter with the same number of parameters as the unknown system, i.e. opt.

This problem arises in many applications, for example control of some machinery plant, or of acoustic and electrical echoes in telecommunications. The Wiener solution is found by minimising the mean-square error between z[k] and y[k], where y[k] is the output of the optimum ?lter driven by x[k]. The circum?ex is used to denote that the output of the optimum ?lter is an estimate of the output of the unknown system.

If x[k]and n[k] are assumed to be uncorrelated stationary random discrete signals then the mean square error is de?ned as

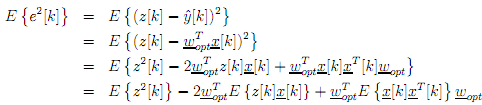
where {·} is the statistical expectation operation, which to a ?rst approximation can be considered to be an average. The right hand side of equation (1) contains a vector of crosscorrelation components and a matrix of autocorrelation components, i.e.

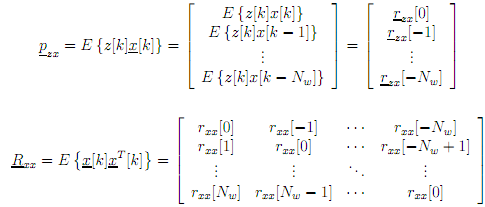
Differenting equation (1) with respect to opt and setting the result to zero yields the optimum Wiener ?lter solution which is given by