Example Solve out the following system of equations.

x² + y ²  = 10

2 x + y = 1

Solution

In linear systems we had the alternative of using either method on any given system.  Along with non-linear systems which will not always be the case. In the first equation both variables are squared and in the second equation both variables are to the first power. In other term, there is no way which we can use elimination here and thus we must use substitution.  Fortunately that isn't too bad to do for this system as we can easily solve the second equation for y and substitute this into the first equation.

y = 1 - 2x

x² + (1 - 2 x )²  = 10

It is a quadratic equation which we can solve.

x² + 1 - 4 x +4 x2  = 10

5x² - 4 x - 9 = 0

( x + 1) (5x - 9) = 0     ⇒ x = -1, x = 9 /5

Thus, we have two values of x.  Now, we have to determine the values of y and we are going to ought to be careful to not make a common mistake here. We find out the values of y by plugging x into our substitution.

x = -1  ⇒      y = 1 - 2 (-1) = 3

x = 9/5 ⇒    y = 1 - 2 (9/5) = - 13/5

Now, only we have two solutions here.  Do not just begin mixing & matching all possible values of x & y into solutions. We get y = 3 as a solution ONLY if x = -1 and hence the first solution is, x = -1, y = 3

Likewise, we just get y = - 13/5 ONLY if x = 9/5 and so the second solution is,

                                                     x = 9 /5, y = - 13/5

Thus, we have two solutions. Now, as noted at the start of this section these two solutions will show the points of intersection of these two curves. As the first equation is a circle and the second equation is a line have two intersection points is definitely possible.  Following is a sketch of the two equations as a verification of this.

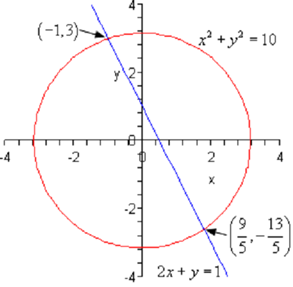
Note that while the two equations are a line & a circle as in the previous example we know that we will contain at most two real solutions as it is only possible for a line to intersect a circle zero, one, or two times.