Fact
Following any system of equations there are accurately three possibilities for the solution.
1. There will not be a solution.
2. There will be just one solution.
3. There will be infinitely many solutions.
It is exactly what we found the possibilities to be while we were looking at two equations. It just turns out that it doesn't matter how several equations we've got. Still there are only these three possibilities.
Now, let's see how we can recognize the first & last possibility while we are using the augmented matrix method for solving. In the earlier section we stated that we desired to employ the row operations to convert the augmented matrix into the following form,
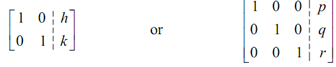
based upon the number of equations exist in the system. It turns out that we ought to have added the qualifier, "if possible" to this instruction, since it isn't always probable to do this. Actually, if it isn't possible to put it into one of these forms then we will know that we are in either the first or last opportunity for the solution to the system.
Before getting into some instance let's first address how we knew what the solution was depend on these forms of the augmented matrix. Let's work along with the two equation case.
Since,

is an augmented matrix always we can convert back to equations. Each of rows represents an equation & the first column is the coefficient of x into the equation whereas the second column is the coefficient of the y in the equation. The final column is the constant which will be on the right side of the equation.
Therefore, if we do that for this case we get,
(1) x + (0) y = h ⇒ x = h
(0) x + (1) y = k ⇒ y = k
and it is exactly what we said the solution was in the previous section.
This idea of turning an augmented matrix back to equations will be significant in the following examples.
Speaking of which, let's go further on and work a couple of examples. We will begin out along with the two systems of equations which we looked at in the first section which gave the special cases of the solutions.