Explain Hall effect.

Consider a slab of material wherein there is a current density J resulting by an applied electric field Ex in the x- direction. The electrons will drift along with an average velocity V‾_x in the x direction; while a magnetic field of flux density B_z (wb/m²) is superposed upon the applied electric field in the Z direction the electrons will experience a Lorentz force perpendicular to V‾_x and to B_z; the magnitude of this force will be specified by B_z (µx)e.

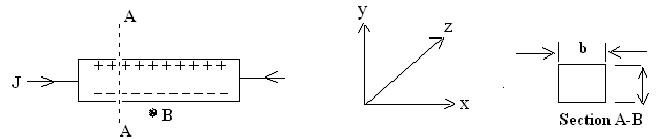
Thus the electrons are driven towards one face in the sample resulting in an excess of electrons near one face and a deficiency of electrons near the other face. These charges will in turn create a counteracting electric field E_y in the y-direction. E_y would build up, till this is of sufficient magnitude to compensate the lorentz force exerted on the electrons because of the magnetic field we may hence write e E_y =B_z e( V‾_x ). In steady state, a Hall voltage, V_H, is thereby put in the y-direction specified by

V_H = E_y .a =B_z (V‾_x), a

The current density in the sample is specified with:

J_x = N. e (V‾_x)

Here N=number of conduction electrons/m³

The current density can be computed from the total current and the cross section (a x b) of the sample.

Therefore,

J_x = I/a x b = N. e (V‾_x)

I = N. e (V‾_x) a x b   ....................................(1)

V_H = B_Z (V‾_x) . a    ......................................(2)

Eliminating (V‾_x) from equating (1) and (2) we get:

V_H = I/(N.e.b)

= (1/N.e) ((B_Z.I)/b)

The ratio + (1/N.e) = Ey/(J_X.B_Z) should be constant.

Another variable that is frequently used to explain the Hall Effect is the ratio of the currents J_Y to J_X.

This is termed as the Hall angle and is denoted with θ θ = JY / JX = σ EY / JX

= σ RH BZ

= µ H BX

Here µ H is termed as the Hall mobility. The hall angle is equal to the average no. of radians traversed through a particle between collisions.