Exceptional cases - Orthographic Projection
1) We have an Orthographic projection, if f=0, then cot (β) =0 that is β=900.
2) β =cot-1 (1)=450 and this Oblique projection is called Cavalier projection, if f=1, the edge perpendicular to projection plane are not foreshortened.
3) β =cot-1 (1/2)=63.4350 and this Oblique projection is called Cabinet projection, if f=1/2 (the foreshortening is half of unit vector).
Note: The usual values of θ are 30° and 45°. The values of (180° - θ) are also suitable.
For foreshortening factor that is f=1, 7/8,3/4,5/8,1/2, an Oblique projections, along with θ=450 is shows in the following figure.
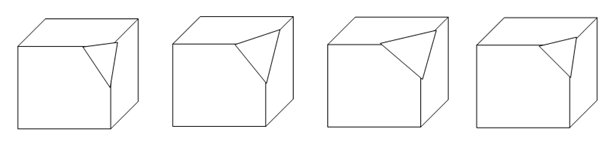
Figure: Oblique projections for f=1,7/8,3/4,5/8,1/2, with θ=450 (from left to right)