Using synthetic division do following  divisions.

Divide 2x³ - 3x - 5  by x + 2

Solution

Okay in this case we have to be a little careful here. We have to divide by a term in the form x - r in order for this to work & that minus sign is absolutely needed.  Thus, we're first going to need to write x + 2 as,

                                             x+ 2 = x - ( -2)

and in doing thus we can see that r = -2 .

Now we can do synthetic division & this time we'll just put up the results & leave it to you to verify all the actual numbers.

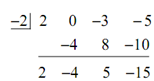
Thus, in this case we have,

2 x³ - 3x - 5 =( x+ 2)(2 x² - 4 x + 5) -15

So, just why are we doing this? One answer is that, down the road in a later section, we are going to wish for get our hands on the Q(x).  Just why we might want to do that will have to wait for an explanation until we get to that point.

Let's start out with the division algorithm.

                                         P ( x)=( x - r ) Q ( x )+ R

Now, let's evaluate the polynomial P(x) at r.  If here we had an actual polynomial we could evaluate P(x) directly for sure, but let's employ the division algorithm and see what we get,

            P ( r)=( r - r) Q ( r )+ R

                      =(0) Q ( r)+ R

                             = R

Now, that's suitable. The remainder of division algorithm is also the value of the polynomial evaluated at r. thus, from our earlier examples now we know the following function evaluations.

If P ( x)= 5x³ - x²+ 6 then P ( 4) =310

If P ( x)= 2 x³ - 3x - 5 then P ( -2)=-15

If P ( x ) = 4 x⁴ -10 x² + 1 then P (6)= 4825

It is a very quick method for evaluating polynomials.  For polynomials along with only a few terms and/or polynomials along "small" degree it may not be much quicker that directly evaluating them.  Though, if there are several terms in the polynomial & they contain large degrees it can be much quicker & much less prone to mistakes than calculating them directly.