Example :  Solve (x+ 1 / x - 5 )≤ 0 .

Solution

Before we get into solving these we need to point out that these don't solve in the similar way which we've solve equations which contained rational expressions.  Along with equations the first thing which we always did was clear out the denominators by multiplying by the least common denominator. That won't work along with these however.

As we don't know the value of x we can't multiply both of the sides by anything which contains an x. Recall that if we multiply both of the sides of an inequality by a negative number we will have to switch the direction of the inequality.  Though, as we don't know the value of x we don't know if the denominator is +ve or -ve and thus we won't know if we have to switch the direction of the inequality or not.  Actually, to make matters worse, the denominator will be both +ve and -ve for values of x in the solution & so that will create real problems.

Thus, we have to leave the rational expression in the inequality.

Now, the basic procedure here is the same as along with polynomial inequalities. The first step is to obatin a zero on one side and writes the other side as a single rational inequality. It has already been done for us here.

The following step is to factor the numerator & denominator as much as possible.  Again, it has already been done in this case.

The following step is to determine where both the numerator and the denominator are zero.  In this case these values are.

                                 numerator : x= -1          denominator : x = 5

Now, we have these numbers for many reasons.  First, just like with polynomial inequalities these are the only numbers where the rational expression might change sign.  Thus, we'll construct a number line using these points to mention ranges out of which to pick test points just like we did along with polynomial inequalities.

There is another cause for needing the value of x that make the denominator zero however.  No matter what else is going on here we do have a rational expression and this means we have to avoid division by zero and thus knowing where the denominator is zero will give us the values of x to ignore for this.

Following is the number line for this inequality.

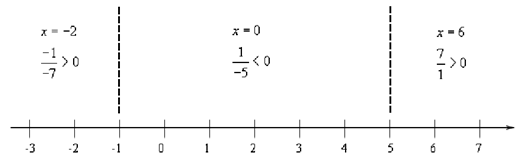
Thus, we require regions which make the rational expression negative. It means the middle region. Also, as we've got an "or equal to" part in the inequality we also have to include where the inequality is zero, thus this means we include x = -1.  Notice that we will also have to avoid x = 5 as that gives division by zero.

The solution for this inequality is following,

                                                           -1 ≤ x < 5                           [-1, 5)

Once again, it's significant to note that we actually do need to test each of the region and not just suppose that the regions will alternate in sign.

Next we have to take a look at some instance that doesn't already contain a zero on one side of the inequality.