Example of Equilibrium:

Express in terms of θ, β and W the force T necessary to hold weight in equilibrium as shown in the figure given below. Also derive an expression for reaction of plane on W. No friction is in between the weight and the plane.

Sol.: As the block is put on the inclined plane, so plane gives vertical reaction on the block say 'R'. Also resolved force 'T' and 'W' in perpendicular and parallel to the plane, now

For equilibrium of the block,

Sum of the components parallel to plane = 0, that is, H = 0

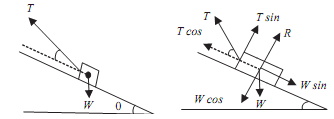
Tcosβ   - Wsinθ = 0                                                                                                                                     ...(i)

Or                         T = Wsinθ  /cosβ         .......ANS

Sum of components perpendicular to plane = 0, i.e.,    V = 0

R + Tsinβ   - Wcosθ   = 0

Or  R = Wcosθ   - Tsinβ                                                                                                           ...(ii)

Putting the value of T in the equation (ii), We get

R = W{cosθ   - sin θ .tanβ  }                                   .......ANS

Hence reaction of the plane = R = W{cos θ-sinθ. tanβ   }             .......ANS