Example Multi-layer ANN with Sigmoid Units - Artificial intelligence:

We will discuss ourselves here with ANNs containing only 1 hidden layer, as this makes describing the back propagation routine simpler. Notice that networks where you may feed in the input on the left and propagate it forward to get an output are known feed forward networks. Below is such an ANN, with 2 sigmoid units in the hidden layer. The weights have been set arbitrarily between all the units.

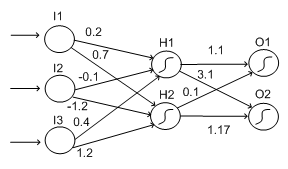
Notice that the sigma units have been recognized with sigma signs in the node on the graph. As we did with perceptrons, we may give this network an input and determine the output. Also we may look to see which units "fired", for example, had a value closer to 1 than to 0.

Imagine we input the values 10, 30, 20 into the 3 input units, from top to bottom. Then the weighted sum approaching into H1 will be:

S_H1 = (0.2 * 10) + (-0.1 * 30) + (0.4 * 20) = 2 -3 + 8 = 7.

Then the σ function is applied to SH1 to give:

σ (S_H1) = 1/(1+e^-7) = 1/(1+0.000912) = 0.999

[Do not forget to -ve S]. In Simple term, the weighted sum coming into H2 will be: S_H2 = (0.7 * 10) + (-1.2 * 30) + (1.2 * 20) = 7 - 36 + 24 = -5

And σ applied to SH2 gives:

σ (S_H2) = 1/(1+e⁵) = 1/(1+148.4) = 0.0067

From this, we may see that H1 has fired, but H2 has not fired. Now we can calculate that the weighted sum put in to output unit O1 will be:

S_O1 = (1.1 * 0.999) + (0.1*0.0067) = 1.0996

And the weighted sum put in to output unit O2 will be: S_O2 = (3.1 * 0.999) + (1.17*0.0067) = 3.1047

Now the output sigmoid unit in O1 will calculate the output values from the network for O1:

σ (S_O1) = 1/(1+e-1.0996) = 1/(1+0.333) = 0.750

and the output from the network for O2:

σ(SO2) = 1/(1+e-3.1047) = 1/(1+0.045) = 0.957

Thus, if this network represented the learned rules for a categorization problem, the input triple (10,30,20) would be categorized into the category related with O2, because this has the bigger output.