Evaluate total extraction:

The steel tie rod 50mm in diameter and 2.5m long is subjected to pull of 100 KN. To what length the rod must be bored centrally so that total extraction will increase by 15 percent under the same pull, bore being 25mm diameter? For steel modulus of elasticity is 2 × 105 N/mm².

Sol.: Diameter of steel tie rod = 50 mm = 0.05 m

Length of steel rod, L = 2.5 m
Magnitude of the pull, P = 100 kN Diameter of bore = 25 mm = 0.025 m Modulus of elasticity, E = 200 × 109  N/m²

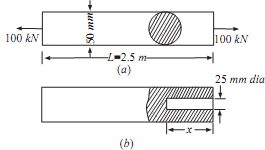
Let length of bore be 'x'. Stress in solid rod   σ= P/A

= {(100 × 1000)/[(   /4)(0.05)²]} = 50.92 × 106  N/m²

Elongation of rod  δ L =   σL/E

= (50.92 × 106  × 2.5) / (200 × 109)

= 0.000636m = 0.636mm

Elongation after rod is bored = 1.15 × 0.636 = 0.731mm

Area of reduction section = (  ? /4) (0.052  - 0.0252) = 0.001472m²

Stress in reduced section σ        b  = (100 × 1000)/0.001472m²

= 67.93 × 106  N/m²

Elongation of rod

=     σ(2.5 - x)/E  +  σb.x/E = 0.731 × 10^-3

= [50.92 × 10⁶ (2.5 - x)]/(200 × 10⁹) +  (67.93 × 10⁶)/(200 × 10⁹) = 0.731 × 10^-3

x = 1.12m

Hence length of bore = 1.12m                                                                             .......ANS