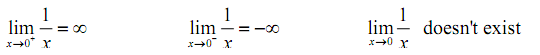Evaluate following limits.

Solution

Therefore we will taking a look at a couple of one-sided limits in addition to the normal limit here.

In all three cases notice as well that we can't just plug in x = 0 .  If we did we would get division by zero.  Also remember again that the definitions above can be easily modified to give similar definitions for the two one-sided limits which we'll require here.

Now, there are many ways we could proceed here to obtain values for these limits. One way is to plug in some points & see what value the function is approaching.  In proceeding section we said that we were no longer going to perform this, however in this case it is a good way to demonstrate just what's going on with this function.

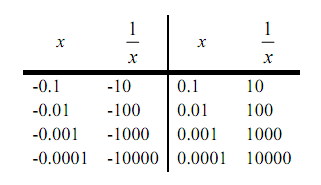
Hence, following is a table of values of x's from both the left & the right.  By using these values we'll be capable to estimate the value of the two one-sided limits & once we have that done we can employ the fact that the normal limit will exist only if the two one-sided limits exist and have the similar value.

Through this table we can notice that as we make x smaller & smaller the function 1/x gets larger & larger and will reach the similar sign that x originally had.  It has to make sense that this trend will keep on for any smaller value of x that we select to use. The function is a constant (one in this case) divided by an increasingly small number. The resulting fraction has to be an increasingly large number and as illustrious above the fraction will retain the similar sign as x.

We can make the function as large and positive as we desire for all x's adequately close to zero whereas staying positive (i.e. on the right).  Similarly, we can make the function as large and -ve as we desire for all x's sufficiently close to zero whereas staying negative (that means on the left). Thus from our definition above it looks like we ought to have the following values for the two one sided limits.

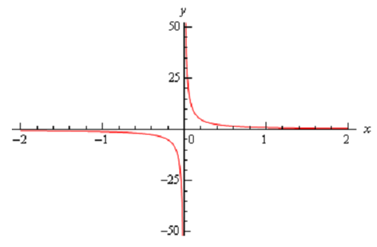
Another way to illustrates the values of the two one sided limits here is to graph the function.  Again, in the earlier section we mentioned that we won't do this too frequently as most functions are not something we can quickly sketch out in addition to the problems with accuracy in reading values off the graph.  In this case though, it's not too difficult to sketch out a graph of the function and, in this case as we'll see correctness is not really going to be an issue.  Hence, here is a quick sketch of the graph.Hence, we can see through this graph that the function does behave much as we specified that it would from our table values. The closer x gets to zero through the right the larger (in the positive sense) the function gets, whereas the closer x gets to zero through the left the larger (in the negative sense) the function gets.

At last, the normal limit, in this case, will not exist as the two one-sided limits have different values.

Hence, in brief here are the values of the three limits for this example.