Evaluate both of the following limits.

Solution : Firstly, the only difference among these two is that one is going to +ve infinity and the other is going to negative infinity.  Sometimes this small difference will influence then value of the limit and at other times it won't.

Let's begin with the first limit and since with our first set of examples it may be tempting to just "plug" in the infinity.  As both the numerator & denominator are polynomials we can use the above fact to find out the behavior of each.  Doing this gives,

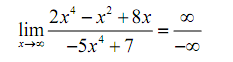
This is still another indeterminate form.  In this case we may be tempted to say that the limit is infinity (due to the infinity in the numerator), zero (due to the infinity in the denominator) or -1 (since something divided by itself is one). There are three separate arithmetic "rules" at work here & without work there is no way to know which "rule" will be accurate and to make matters worse it's possible that none of them might work and we might obtain a completely different answer, say -2/5 to pick a number totally at random.

Hence, when we have a polynomial divided by a polynomial we will proceed much as we did with only polynomials. First we identify the largest power of x in the denominator (and yes, we just look at the denominator for this) and then we factor this out of the numerator and denominator both.  Doing this for the first limit gives,

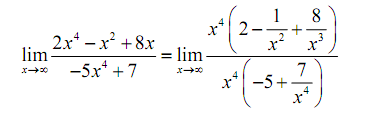
Once we've done it we can cancel the x^- from the numerator and the denominator both and then utilizes the Fact 1 above to take the limit of all the remaining terms. it gives,

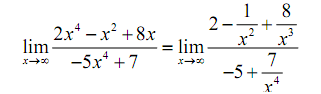
=  2 + 0 + 0 / -5 + 0

= - 2 /5

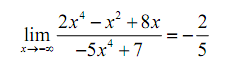
In this the indeterminate form was neither of the "obvious" option of infinity, zero, or -1 so be careful with make these kinds of supposition with this kind of indeterminate forms.

The second limit is done in alike fashion.  However, Notice that nowhere in the work for the first limit did we in fact use the fact that the limit was going to plus infinity.  In this it doesn't matter which infinity we are going towards we will obtain the similar value for the limit.