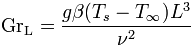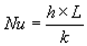The objective of the research is to empirically develop correlations between convection heat transfer and these above mentioned non-dimensional in numbers. The simple empirical correlation of Nusselt Number with Grashof/Rayleigh numbers in natural convection from a surface is given by following equation.
Geometry:
Geometric model of cubicle and enclosures with an opening of following dimensions would be constructed using CAD software SolidWorks. Five different sizes of openings (one at a time) are evaluated for convection heat loss. The dimensions of the enclosure, openings and its locations are as follows.
Cubical Enclosure - 5m x 5m x 5m
Opening sizes - (1mx 5m), (2m x 5m), (3m x 5m) and (4m x 5m)
|
Nu
|
Nusselt Number
|
|
GrL
|
Grashof number
|
|
Pr
|
Prandtl number
|
|
Ra
|
Rayleigh number
|
|
C
|
Constant Coefficient
|
|
g
|
acceleration due to Earth's gravity
|
|
ß
|
volumetric thermal expansion coefficient (equal to approximately 1/T, for ideal fluids, where T is absolute temperature)
|
|
Ts
|
surface temperature
|
|
T∞
|
Temperature bulk air
|
|
L
|
Distance between hot and cold surface in our case bottom and top surface
|
|
D
|
diameter
|
|
v
|
Kinematic viscosity
|
|
k
|
thermal conductivity of the fluid
|
|
h
|
convective heat transfer coefficient
|
|
ρ
|
Density of the fluid
|
|
T2
|
Temperature of the top wall
|
|
L1
|
length of opening
|
|
L
|
Total length of the enclosure
|
Location of opening- On one wall of the enclosure the opening starting from the bottom of the wall
Heat - Bottom surface uniformly heated by a source with 2000W of heat
CFD will be done by ANSYS or Solidworks FlowWorks
Mathematical model:
The target equation is Nu= C. RaLx . Pry . (L1/L)
The value of Nu and Ra obtained for the simulation will be plotted. From this equation we can find the values of C, x and y which will give us the required relation.
The simple empirical correlation of Nusselt Number with Grashof/Rayleigh numbers in natural convection from a surface is given by following equation.
Nu= f {GrL. Pr} (Nusselt Number is a function of Grash of & Prandtl number)
Ra = GrL. Pr