The modified duration is a measure of the sensitivity of a bond's price to interest rate changes; the assumption made here is that the expected cash flow does not change with the interest rates. In the case of a callable bond, the cash flow does change with the interest rates. The modified duration may not be appropriate to measure the price volatility of such bonds. If the rate of interest falls, the expected cash flow for a callable bond may change. Thus, it may be concluded that modified duration is not an appropriate measure of price sensitivity to interest rate changes.

If P₀ is the initial price and P₁ is the price level to which it is reduced on account of a small increase in the yield (D_y) and the price increases to a level of P₂ on account of a small decrease in the yield (D_y) then the approximate duration is given by the formula,

         Approximate duration =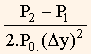 

Where,

         y is used in the decimal form.

It can be observed that the formula measures the average percentage price change relative to the initial price per basis point change in the yield.

When this formula is used for a non-callable bond, it gives the modified duration since there is no change in the cash flow due to change in the yield. But when this formula is used for a callable bond, i.e., a bond embedded with an option, the new prices at the higher and lower yield levels should reflect the value from the valuation model. Duration calculated in this method is called effective duration or option-adjusted duration.

We may summarize the relationships among the duration, modified duration and the effective duration on the following lines:

• Duration is a generic concept that indicates a bond's response to a change in interest rates.

• Modified duration is a measure of duration in which it is assumed that the cash flows do not change with change in the yield.

• Effective duration measures the sensitivity of a bond's price considering that the expected cash flows change on account of changes in the yield due to the option available with it.

Another measure that is normally studied along with duration is convexity. The standard convexity measure may be inappropriate for a bond with embedded options as it does not consider the effect of a change in interest rates on the bond's cash flow. The formula for calculating the approximate convexity of any bond is,

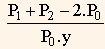
When the prices used in this formula are calculated assuming that the cash flows do not change when yields have changed, the resulting convexity becomes a good approximation of standard convexity. On the other hand, if prices are calculated under the assumption that the cash flows have undergone a change due to changes in the yield in respect of a callable bond, then it is called effective convexity.