Effective Branching Rate:
Assessing heuristic functions is an important part of "AI" research: a particular heuristic function may sound such a good idea, but in practice give no discernible increase in the quality of the search. Search quality can be estimated experimentally in terms of the output from the search, so by using various measures such as the effective branching rate. Let suppose a particular problem P has been solved by search strategy S by expanding N nodes, and the solution play at depth D in the space. Then the effective branching rate of S for P is calculated by comparing S just to a uniform search U. The other example of a uniform search is a breadth first search where the number of branches from any node is always the same (as in our baby naming example). After that we suppose the (uniform) branching rate of U is like that, on the exhausting its search to depth D, it too would have expanded exactly N nodes. That should be imagined branching rate, written b*, is the effective branching rate of S and is calculated thus:
N = 1 + b* + (b*)2 + ... + (b*)D.
Rearranging this equation will give a proper value for b*. For example if we considered that we taken from Russell and Norvig rule, suppose S finds a solution at depth 5 having expanded 52 nodes. As in the above this case:
52 = 1 + b* + (b*)2 + ... + (b*)5.
and it turns out that b*=1.91. To calculate this, we can use the very well known mathematical character:
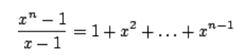
This enables us to write a polynomial for which b* is a zero, and we can solve this using numerical techniques like Newton's method.
It is normally the case that the effective branching rate of a search strategy is similar over all the problems. It is may be used for, so that it is acceptable to average b* over a small set of problems to give a valid account. If there is a heuristic search has a branching rate near to 1, then this is a good sign. We state that one heuristic function h1 dominates another h2 if the search using h1 always has a lower effective branching rate than h2. Having a lower effective branching rate is clearly desirable because it means a quicker search.