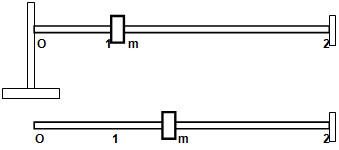
You are required to investigate the dynamic movement of a mass m sliding along a rod as shown in the diagram below. The rod is rotating at a constant angular velocity θ. The mass m is able to slide along the rod from position 1 (given by r = r1 to position 2 given by r = r2). At position 2 there is a stop as shown on the figure .Initially, at time t = 0, the mass m is tied by a string to the centre of rotation O which is then suddenly cut and frees the mass. At time t = 0, the angular position of the rod is θ = 0 rad. You are to neglect friction and the mass of the rod.

Notes:
Your own values of , r1, r2 and m are given in your Data Sheet

This investigation is to be carried out with your own specific data provided on a separate Data Sheet. No written material such as paragraphs or parts of text should be copied from any other source including your fellow students. All written text should be your own work.

Your tasks and corresponding marking scheme are as follows:

A. Draw the free body diagram of the forces on mass m at a position r between r1 and r2 and deduce the expressions for ar and aθ.

B. Determine the values of radial and tangential accelerations at position 1 just after cut-off of the string.

C. Determine the expressions for radial and tangential velocities for the mass m at any position r between r1 and r2.

D. Deduce the speed of the mass m when reaching position 2 and calculate the corresponding force involved when it stops at 2.

E. At t = 0.01 s, determine the angular and radial position of the mass as well as all the components of radial and tangential velocities and accelerations.

F. Explain why there is no such a thing as a centrifugal force.

G. If friction had been taken into account, what would be the relevant equations of motion. (do not solve them).

H. Report structure & presentation.