Difference between absolute and relative in the definition

Now, let's talk a little bit regarding the subtle difference among the absolute & relative in the definition above.

We will consist of an absolute maximum (or minimum) at x = c provided f(c) is the largest (or smallest) value that the function will ever take on the domain that we are working on.  Also, while we say the "domain we are working on" this just means the range of x's which we have selected to work with for a specified problem.  There might be other values of x that actually we can plug into the function however have excluded them for some cause.

A relative maximum or minimum is slightly different. All that's needed for a point to be a relative maximum or minimum is for that point to be maximum or minimum within some interval of x's around x = c .  There might be larger or smaller values of function at some other place, however relative to x = c , or local to x = c ,  f(c) is larger or smaller than all the other function values which are near it.

 Note that in order for a point to be a relative extrema we have to be able to look at function values on both sides of x = c to distinguish if it really is a maximum or minimum at that point. It means that relative extrema do not takes place at the end points of a domain.  They can only takes place interior to the domain.

There is in fact some debate on the preceding point. Some of the folks feel that relative extrema can takes places on the ending points of a domain.  Though, in this class we will be utilizing the definition that says that they can't takes place at the end points of a domain.

Usually it's easier to obtain a feel for the definitions by taking a look at a graph.

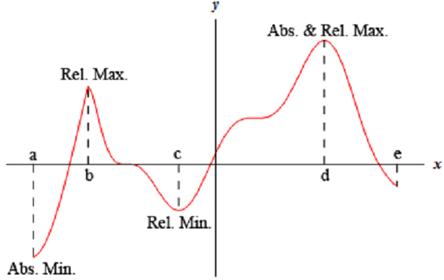
For the function illustrated in this graph we have relative maximums at x =b & x = d .  Both of point is a relative maximum as they are interior to the domain illustrated and are the largest point on the graph in some interval about the point. We also have a relative minimum at x = c as this point is interior to the domain & is the lowest point on the graph in an interval around it. The far right end point, x = e , will not be a relative minimum as it is an ending point.

The function will contain an absolute maximum at x = d & an absolute minimum at x = a .

These two points are the largest & smallest that the function will ever be. We can also note that for a function the absolute extrema will takes place at either the endpoints of the domain or at relative extrema. 

Let's see some instances to ensure that we have the definitions of absolute extrema & relative extrema straight.