Determine the maximum stress developed in the beam:

An I section in Figure is utilized as a beam. The beam is subjected to a bending moment of 2.5 kN m at its neutral axis. Determine the maximum stress developed in the beam.

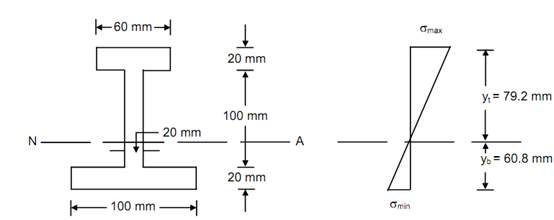
Beam Section                                 Bending Stress Distribution

Figure

Solution

 Assume 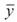be the distance of centroid from the bottom face.

Then, 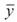  =∑ ay / ∑ a

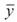   = ((100 × 20) ×10 + (20 ×100) × 70 + (60 × 20) ×130) /((100 × 20) + (20 ×100) + (60 × 20))

= 60.8 mm

 Moment of inertia of the section around the horizontal axis passing through the centriod,

I = [(1/12) ×100 × (20)³ + (100 × 20)(60.8 - 10)² ]

+[ (1/12) × 20 (100)³ + (20 ×100)(70 - 60.8)² ]

+ [(1/12) × 60 (20)³ + (60 × 20)(130 - 60.8)² ]

= 1285.04 × 10⁴ mm4

Topmost layer distance, y_t = 140 - 60.8 = 79.2 mm

Bottommost layer distance, y_b = 60.8 mm

∴          y_max = y_t = 79.2 mm

 Through the relation,  M/ I = σ/ y

We obtain,       σ_max = ( M/ I) × y_max

Bending moment,  M = 2.5 kN m

                                   = 2.5 × 10⁶ mm

∴          σ_max =  (2.5 × 10 ⁶/1285.04 × 10⁴)  × 79.2 = 15.41 N/mm

∴  The maximum bending stress in the beam = 15.41 N/mm².