Determine the maximum bending moment:

A 12 m span simply supported beam is carrying a consistently distributed load of 2 kN/m over a length of 6 m from the left end and point loads 6 kN, 3 kN and 4 kN at distances of 7 m, 8 m and 9 m, respectively. Draw BM diagram and SF diagram for the beam and determine the maximum bending moment.

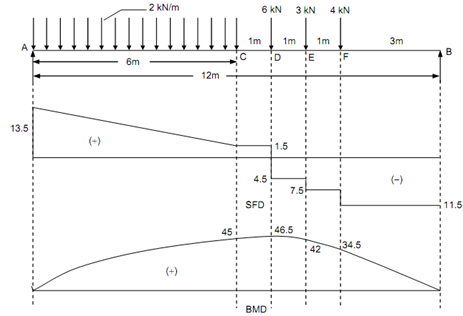
Figure

Solution

Taking moments around A, and equating to zero.

R_B × 12 - (4 × 9) - (3 × 8) - (6 × 7) - 2 × 6 ×(6/2)   = 0

Therefore,        R_B = 11.5 kN, and

R_A = (2 × 6) + 6 + 3 + 4 - R_B = 25 - 11.5 = 13.5 kN

Shear Force (beginning from the left end)

 SF at A, FA = + 13.5 kN

SF at C, FC = + 13.5 - 2 × 6 = + 1.5 kN

SF just left of   D = + 1.5 kN

 SF just right of D = + 1.5 - 6 = - 4.5 kN

SF just left of  E = - 4.5 kN

SF just right of E = - 4.5 - 3 = - 7.5 kN

 SF just left of   F = - 7.5 kN

SF just right of F = - 7.5 - 4 = - 11.5 kN

SF just left of   B = - 11.5 kN = Reaction at B.

Bending Moment

BM at A, MA = 0

BM at C, M  = (13.5 × 6) - 2 × (6 ×(6/2))   = 45 kNm (considering left side)

BM at D, MD = (11.5× 5) - (4 × 2) - (3 × 1) = 46.5 kN m (considering right side)

BM at E,

M_E = (11.5 × 4) - (4 × 1) = 42 kN m

BM at F,

M_F = (11.5 × 3) = 34.5 kN m

The maximum bending moment take place at D where the shear force changes sign.

                       M_max = 46.5 kN m.