Determine the inverse transform of each of the subsequent.
(a) F(s) = (6/s) - (1/(s - 8)) + (4 /(s -3))
(b) H(s) = (19/(s+2)) - (1/(3s - 5)) + (7/s2)
(c) F(s) = (6s/(s2 + 25)) + (3/(s2 + 25))
(d) G(s) = (8/(3s2 + 12)) + (3/(s2 - 49))
Solution
I've always felt as the key to doing inverse transforms is to find the denominator and attempt to identify what you've found based on that. If there is simply one entry in the table which has that exact denominator, the subsequent step is to ensure the numerator is correctly set up for the inverse transform process. If this isn't, accurate this, it is always easy to do and after that take the inverse transform.
If there is more than one entry into the table has an exact denominator, so the numerators of each will be dissimilar, then go up to the numerator and see that one you've found. If you require correcting the numerator to find it into the accurate form and then take the inverse transform.
Therefore, with this advice in mind let's notice if we can take some inverse transforms.
(a) F(s) = (6/s) - (1/(s - 8)) + (4 /(s -3))
From the denominator of the primary term this seems as the first term is just a constant. The accurate numerator for such term is a "1" thus we'll just factor the 6 out before taking the inverse transform. The next term comes out to be an exponential along with a = 8 and the numerator is exactly what this requires to be. The third term also appears to be an exponential, only now a = 3 and we'll require to factor the 4 out before taking the inverse transforms.
Therefore, with a little more detail than we'll generally put in these,
F(s) = 6 × (1/s) - (1/(s - 8)) + 4 × (1/(s - 3))
= f(t) = 6(1) - e8t + 4e3t
= = 6 - e8t + 4e3t
(b) H(s) = (19/(s+2)) - (1/(3s - 5)) + (7/s2)
The first term under this case seems as an exponential along with a = -2 and we'll require to factor out the19. Be alert along with negative signs in such problems, it's extremely simple to lose track of them.
The second term almost seems as an exponential, except as it's got a 3s in place of just an s in the denominator. This is an exponential, but under this case we'll require to factor a 3 out of the denominator before containing the inverse transform.
The denominator of the third term seems to be #3 in the table along with n = 4. The numerator though, is not correct for this. There is presently a7 in the numerator and we require a 4! = 24 in the numerator. It is very simple to fix. Whenever a numerator is off through a multiplicative constant, as under this case, all we require to do is put the constant that we require in the numerator. We will just require remembering to take it back out by dividing by similar constant.
Therefore, let's first rewrite the transform.
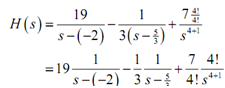
Therefore, what did we do now? We factored the 19 out of the primary term. We factored the 3 out of the denominator of the second term as this can't be there for the inverse transform and in the third term we factored all things out of the numerator except the 4! As which is the portion which we need in the numerator for the inverse transform method or process.
Let's here take the inverse transform.
h(t) = 19 e-2t - ((1/3) e(5t/3)) + (7/24)t4
(c) F(s) = (6s/(s2 + 25)) + (3/(s2 + 25))
Under this part we've got similar denominator in both terms and our table implies us that we've either found #7 or #8. The numerators will imply us that we've in fact got. The first one has an s in the numerator and therefore this implies that the first term should be #8 and we'll require factoring the 6 out of the numerator under this case. The second term has merely a constant in the numerator and thus this term must be #7, though, in order for this to be exactly #7 we'll require multiply/divide a 5 in the numerator to find it accurate for the table.
The transform turns into,
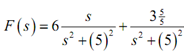
F(s) = 6 × (s/(s2+ 52)) + ((3/5) (5/(s2 + 25)))
Taking the inverse transform provides,
f(t) = 6 cos(5t) + (3/5) sin(5t)
(d) G(s) = (8/(3s2 + 12)) + (3/(s2 - 49))
Under this case the first term will be a as once we factor a 3 out of the denominator, whereas the second term seems to be a hyperbolic sine (#17). Again, be cautious with the difference among these two. Both of the terms will also require having their numerators fixed up. Now there is the transform once we're done rewriting this.
G(s) = (1/3)(8/(s2 + 4)) + (3/(s2 - 49))
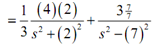
Remember that in the first term we took gain of the fact that we could find the 2 in the numerator that we required through factoring the 8. The inverse transform is after that,
g(t) = (4/3) sin(2t) + (3/7) sinh(7t)
Thus, probably the best method to identify the transform is through looking at the denominator. If there is more than one option use the numerator to know the accurate one. Fix up the numerator if required to get it in the form required for the inverse transform process. At last, take the inverse transform.