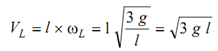Determine the angular-velocity of uniform bar:
A uniform bar of length l and mass M is hinged at its end B and is released from its horizontal position BA. Determine its angular-velocity at any angle θ with BA and at the instant while it is vertical where A2 is the lowest position of end A.
Solution
The bar BA being of uniform size and mass has its weight (W) at its mid-point and it undergoes a motion of rotation about axis at B. Note that this axis of rotation is horizontal (i.e. perpendicular to the plane of the paper) since motion of rotation is in vertical plane.
When the bar takes any position BA1 at an ∠ θ, the C. G. of bar comes down vertically by (l/2) sin θ . Applying the principle of conservation of energy, letting the datum level as AB, since initial angular velocity in position BA is zero,
Initial total energy = PE of (BA) + KE in position (BA)
= 0
Total energy in position (BA1) = PE (BA1) + KE (BA1)
= - ( Mg(l/2) sin θ )+ (I (m) (ω1)2 )/2
PE (BA1) is negative since its CG is below datum level and ω1 is angular velocity of the bar when A reaches A1.
As per the principle,
∴ I (m) (ω1)2 /2- Mg(l/2)sin θ = 0
Ml2/3× (ω1)2 /2 = Mg (l/2) sin θ
∴(ω1)2 = (3 g sin θ)/l
At lowest position BAL when θ = 90o.
(ωL)2 = 3 g/l
Linear velocity of the lowest point AL is in horizontal direction and its magnitude is given by